
Clase 8 - Ejes Radicales
Esperamos sus mails en educabri@oma.org.ar.
Clase 8 - Ejes Radicales
Esperamos sus mails en educabri@oma.org.ar.
Antes de comenzar esta clase deberían asegurarse de saber bien potencia de un punto, tema tratado en la clase 6 del curso Educabri 2000, pues es fundamental para entender ejes radicales.
Al final de esta clase hay una encuesta para ver que tal les parecieron los temas que tratamos, si los problemas fueron o no difíciles, etc. Por favor complétenla, porque las clases son para ustedes y si no tenemos respuesta del otro lado no podremos ir mejorándolas. No se olviden!!!
Para empezar, un problemita ...
Sean C1 y C2 dos circunferencias exteriores entre sí y sean P y Q en C1 de modo que PQ es diámetro de C1 y tal que no estén sobre la recta que une los centros de ambas circunferencias. Construir un diámetro RS de C2 de modo que PQRS sea un cuadrilátero cíclico (o sea, existe una circunferencia que pasa por los cuatro vértices de PQRS).
Si no les salió, no importa. Después volvemos al problema. Veamos ahora un poco de teoría.
Dadas dos circunferencias, C1 y C2, se llama eje radical al lugar geométrico de los puntos cuya potencia con respecto a C1 y con respecto a C2 es la misma.
Les adelantamos, que el eje radical es una recta perpendicular a la recta que pasa por los centros de ambas circunferencias. Veamos como se construye y por qué es una recta.
Creen dos circunferencias exteriores, C1 y C2 (de radios a y b respectivamente), sus centros, y una recta básica r.
Construyan dos puntos, T y T1, sobre la recta, para elegir la medida de las tangentes.
Tracen la perpendicular a r por el centro de C y marquen sus intersecciones con C, llamemos M1 a la más próxima a r. Tracen la tangente a C1 por M1 (o sea, una paralela a r por ese punto).
Trasladen el segmento TT1 con vector TM1. Queda el segmento M1M2. Tracen la circunferencia concéntrica con C1 que pasa por M2. En esa circunferencia, están todos los puntos cuya tangente a C1 mide TT1. ¿Por qué?
Hagan la misma construcción (a partir de 3.) para C2.
Construyan las intersecciones de las dos circunferencias que quedaron, P1 y P2. Esos puntos pertenecen al eje radical, porque sus tangentes a C1 y C2 miden TT1.
¿Cuál es el lugar geométrico de P1 y P2 al varias la longitud de TT1? ¿ Qué pasa si C1 y C2 son secantes?
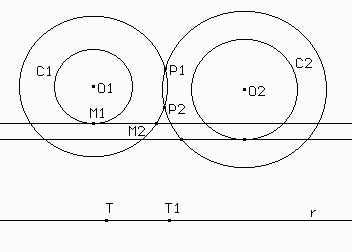
Veamos que el lugar geométrico de P1 y P2 es una recta. Sea A el pie de la perpendicular desde P1 a O1O2. El radio O1M2² = a² + TT1² y O2P1² = b² + TT1². Restando ambas ecuaciones tenemos que O1M2² - O2P1² = a² - b² que es constante. Como O1P1² = O1A² + AP1² y también O2P1² = AO2² + AP1². Restando la segunda ecuación de la primera e igualando tenemos que O1A² - AO2² = (O1A - AO2) (O1A +AO2) = a² - b² que es constante al igual que lo es O1O2. Por lo tanto A es un punto fijo y el lugar geométrico de P1 es la recta perpendicular a O1O2 por A.
Ahora que sabemos lo que es el eje radical y como construirlo volvamos al problema que plantemos al comienzo de esta clase. Si quieren intentar hacerlo nuevamente, es un buen momento.
Si PQ no es perpendicular a la recta que une los centros de C1 y C2 (llamémoslos O1 y O2 respectivamente) entonces la recta PQ intersecará al eje radical de ambas circunferencias, pongamos en A. La recta O2A interseca a C2 en R y S. Les conviene hacerse una Macro para trazar ejes radicales porque sino hacer las construcciones puede tornarse muy pesado. Si no recuerdan como hacer una macro vean la clase 16 del curso Educabri 98.
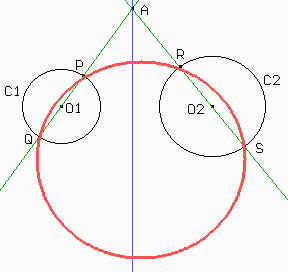
Veamos que PQRS es un cuadrilátero cíclico. Como A pertenece al eje radical de ambas circunferencias entonces AR . AS = AP . AQ, o lo que es lo mismo AR / AQ = AP / AS. Y dado que APR y AQS comparten el ángulo comprendido entonces son semejantes, siendo los ángulos APR = RSQ con lo que QPR + RSQ = 180°. Por tanto PQRS es cíclico.
El caso de que PQ sea perpendicular a O1O2 se los dejamos a ustedes. También les dejamos, como siempre, algunos problemas para que practiquen.
Problemas
1. Mostrar que trazando las cuatro tangentes comunes a dos circunferencias, los puntos medios de los segmentos determinados en cada recta por los puntos de tangencia a las circunferencias, están alineados.
2. Dadas tres circunferencias cuyos centros no están alineados, encontrar el punto que tenga igual potencia con respecto de las tres circunferencias. Ese punto se llama centro radical de las tres circunferencias.
3. ¿Cuál es el lugar geométrico de los puntos desde los que las tangentes a dos circunferencias dadas tienen longitudes iguales?
4. Sean A, B, C y D cuatro puntos distintos sobre una recta, en ese orden. Las circunferencias de diámetros AC y BD se cortan en X e Y. La recta XY corta a BC en el punto Z. Sea P un punto en la recta XY, distinto de Z. La recta CP corta a la circunferencia de diámetro AC en los puntos C y M, y la recta BP corta a la circunferencia de diámetro BD en los puntos B y N. Demostrar que la rectas AM, DN y XY son concurrentes.
Así terminamos la octava clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. Dentro de dos semanas ofreceremos una nueva clase.
Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
|