Clase 8 - Ángulos inscriptos en una circunferencia

Esperamos sus mails en educabri@oma.org.ar.

 

Los ángulos inscriptos en una circunferencia tienen muchas aplicaciones en geometría. En esta clase veremos qué es un ángulo inscipto en una circunferencia, sus propiedades y algunas de sus aplicaciones.

Parte 1 - Actividades

1-1 Ángulo inscripto

1. Construí una circunferencia S con centro O y radio OR.
2. Marcá tres puntos A, B y C en la circunferencia (Point on object).
3. Creá los segmentos AB y BC. Marcá el ángulo ABC y medilo.
4. Mové el punto B por el arco AC, ¿Qué pasa con la medida del ángulo ABC?
5. Colocá ahora B del otro lado del arco AC.
6. ¿Qué pasó con la medida de ABC? ¿Qué relación encontrás entre las dos medidas?
   Sugerencia: mové los puntos A o C y armá una tablita con los pares de valores que vas obteniendo para distintas posiciones de A y C.
7. ¿Cuánto mide el ángulo ABC cuando AC es un diámetro de la circunferencia?

• El ángulo ABC se llama inscripto en la circunferencia S. Observamos que ABC es constante mientras B se mantenga en el mismo arco.

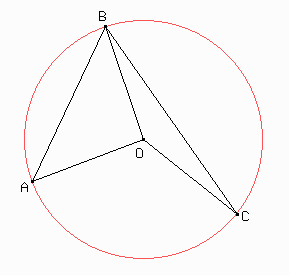
1-2 Ángulo central

1. En la figura anterior, creá los segmentos AO y OC. Marcá el ángulo AOC y medilo.
2. Qué relación hay entre la medida de ABC y la de AOC. De nuevo, te sugerimos que hagas una tablita con distintos pares de valores de ABC y AOC.

• El ángulo AOC se llama ángulo central. Observamos que AOC es el doble de ABC.

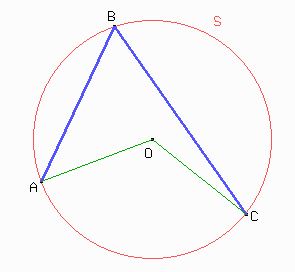
1-3 Ángulo inscripto en una semicircunferencia

1. ¿Cuánto mide AOC cuando AC es diámetro?

En este caso, decimos que el ángulo ABC esta inscripto en una semicircunferencia.

2. Demostrá lo que observaste en el item 7 de la actividad 1-1.
   Sugerencia: usá la actividad 1-2.

Problemas

1. Demostrar las propiedades enunciadas en las actividades 1-1 y 1-2.
Sugerencia: observando los triángulos isósceles de la figura, demostrar primero que ABC mide la mitad de AOC. Deducir que ABC es constante.

Ahora podemos resolver con más generalidad los problema enunciados en la clase 3:
2. ¿Qué propiedad deben cumplir los ángulos de un cuadrilátero para que exista una circunferencia circunscripta a él?

3. Sea ABC un triángulo rectángulo en A. Sea M el punto medio de BC. Probar que MA = MB = MC.

4. Sea S una circunferencia y P un punto exterior a ella. Construir las rectas tangentes a la circunferencia, que pasan por P.

Así terminamos la octava clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet Clase 9	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar