Clase 9 - Más sobre ángulos inscriptos

Esperamos sus mails en educabri@oma.org.ar.

 

Para seguir estas actividades es importante tener bien presente la clase anterior.

Parte 1 - Actividades

1-1 Arco capaz

1. Construí una circunferencia S.
2. Marcá dos puntos A y C en la circunferencia (Point on object). Traza la recta AC.
3. Creá un punto libre B de un lado de la recta AC. Creá los segmentos AB y BC. Marcá el ángulo ABC y medilo.
4. Colocá B sobre la circunferencia y observá la medida del ángulo ABC. (Ya sabemos, por la clase 8, que la medida no va a cambiar al mover B sobre el arco.)
5. Mové B fuera de la circunferencia, sin salir del semiplano determinado por AC. ¿Qué pasa con el ángulo ABC? ¿Y cuándo B está dentro de la circunferencia?
6. ¿Qué conclusión sacás de todo esto? ¿Qué pasa cuando B esta del otro lado de la recta AC?

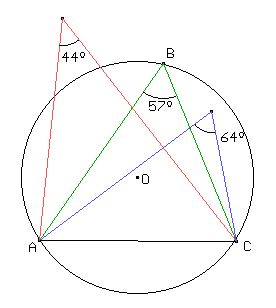
Verificamos que dados dos puntos A y C y un ángulo a, los puntos B tales que ABC = a están sobre dos arcos de circunferencia.

• El lugar geométrico de los puntos P que verifican que los ángulos APB y ABC son iguales se llama arco capaz del ángulo ABC con respecto al segmento AB.

1-2 A igual ángulo, igual arco

1. Construí una circunferencia S.
2. Marcá tres puntos A, B y C en la circunferencia (Point on object).
3. Marcá y medí el ángulo ABC.
4. Mové C, alejándolo de A. ¿Qué pasa con la medida del ángulo ABC?
5. ¿Y si acercás C a A?
6. Mové A y luego C para lograr que la medida de ABC sea igual a la medida inicial.
7. ¿Qué relación hay entre los segmentos AC (inicial) y AC (final).
8. ¿Podés enunciar la propiedad descubierta?

1-3 Bisectriz de un ángulo inscripto

1. Construí una circunferencia S con centro O y radio OR.
2. Marcá tres puntos A, B y C en la circunferencia (Point on object).
3. Construí la bisectriz del ángulo ABC. Nombrá P a la intersección (distinta de B) entre esta recta y S.
4. ¿Qué pasa con P al mover B sobre S?
5. ¿Cómo podrías explicar lo que ves? Sugerencia: notar que como ABC es constante, también ABP y PBC son constantes y usar 1-2.

Problemas

1. Dados tres puntos A, B y C, construir el arco capaz del ángulo ABC con respecto al segmento AC.

2. Dado un segmento AB, construir el arco capaz de 60^o con respecto a AB.

3. Ángulo semi-inscripto
Sean S una circunferencia de centro O y tres puntos A, B y C sobre ella. Se traza por A la recta r, tangente a S (esto es, la perpendicular por A a AO). Probar que el ángulo que forman las rectas AC y r es igual al ángulo ABC.

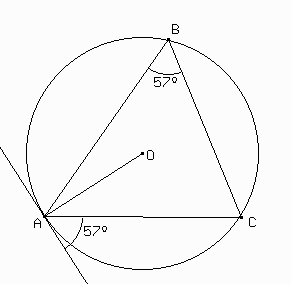
Este ángulo se llama semi-inscripto en la circunferencia.

4. Dados tres puntos I, H, M sobre una circunferencia S, construir un triángulo ABC inscripto en S tal que I sea la intersección de la bisectriz de BAC con S, H la intersección de la altura por A con S y M la intersección de la mediana por A (o su prolongación).

Así terminamos la novena clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet Clase 10	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar