Clase 6 - El ortocentro

Esperamos sus mails en educabri@oma.org.ar.

 

Parte 1 - Actividades

El cuarto y último punto notable del triángulo que estudiaremos es el ortocentro.

1-1 Alturas de un triángulo

Las alturas de un triángulo son las rectas perpendiculares a un lado que pasan por el vértice opuesto..

1. Crear un triángulo ABC.
2. Trazá las alturas del triángulo ABC. Te recomendamos usar el comando perpendicular line.
3. ¿En cuántos puntos se cortan?

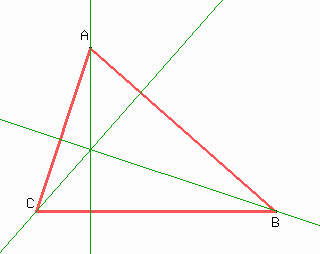
Sí, las alturas siempre se cortan en un punto.

4. ¿Se te ocurre una demostración de esta propiedad?

A primera vista, parece un problema difícil. Pero existe una demostración muy sencilla.

5. Trazá por cada vértice una recta paralela al lado opuesto.
6. Marcá las 3 intersecciones entre estas tres rectas y nombralas P, Q, R.
7. Ahora mirá el triángulo PQR. ¿Qué papel juegan las alturas de ABC en este nuevo triángulo?
8. Demostralo. (Sugerencia: congruencia de triángulos.)

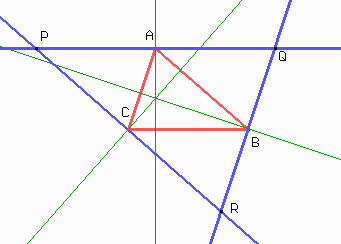
No son ni más ni menos que las mediatrices. Pero ya sabemos que las mediatrices de un triángulo siempre se cortan en un punto. Entonces las alturas de ABC se cortan en un punto. ¡Una hermosa demostración!

1-2 Alturas: ¿rectas o segmentos?

Muchos ya conocemos la fórmula para él área de un triángulo: (base . altura) / 2.

Pero nosotros dijimos que altura era la recta, y la longitud de una recta es infinita. No hay acuerdo. A veces diremos altura para referirnos a la recta y a veces para referirnos al segmento. Sólo aclararemos cuando pueda haber ambigüedad.

Construiremos ahora las alturas como segmentos.

1. Creá un triángulo ABC y trazá las rectas de las alturas.
2. Trazá las rectas AB, BC y AC.
3. Marcá las intereseccion entre la recta AB y la recta perpendicular a AB que pasa por C. Hace lo mismo para BC y A y para AC y B. Nombrá estos puntos como P, Q y R respectivamente.
4. Creá los segmentos PC, QA y RB. Estos son los segmentos buscados.
5. ¿Por qué te pedimos que traces las rectas AB, BC y AC?
6. ¿Es cierto que estos tres segmentos siempre se cortan en un punto? Esa es una de las razones por las que a veces necesitaremos toda la recta.

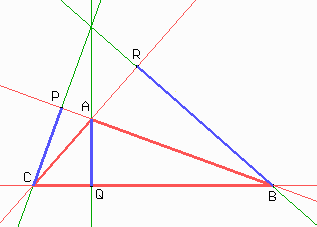
1-3 El ortocentro

• El punto de intersección de las alturas se llamá ortocentro y generalmente se lo nombra H.

1. Marcá el ortocentro de un triángulo ABC.
2. ¿Cuál es el ortocentro de un triángulo rectángulo?
3. ¿Para qué triángulos el ortocentro cae dentro del triángulo y para qué triángulos cae afuera?

Parte 2. Problemas

2-1 Sea ABC un triángulo con el ángulo BAC mayor que 90^o. Sea H el punto de intersección de las alturas. Si el triángulo BCH es equilátero, ¿cuánto mide el ángulo BAC?

2-2 Demostrar que para un punto P en el interior de un triángulo equilátero ABC, la suma de las distancias entre P y cada uno de los lados del triángulo es igual a la altura del mismo.

2-3 Dados cuatro puntos A, B, H y O sobre el plano, construir un punto C tal que H sea el ortocentro y O el circuncentro del triángulo ABC.

2-4 Sean P, Q y R los pies de las alturas (ver la actividad 1-2). ¿Qué papel juegan las alturas del triángulo ABC en el triángulo PQR?

La demostración del último es sencilla utilizando cosas que veremos más adelante. Por ahora, sólo podemos intuir.

Así terminamos la sexta clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet Clase 7	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar