Clase 3 - El circuncentro

Esperamos sus mails en educabri@oma.org.ar.

 

Parte 1 - Actividades

Con las clases anteriores ya sabemos lo suficiente para realizar muchas construcciones. Ahora vamos a empezar a aprender propiedades de las figuras geométricas haciendo construcciones con el Cabri.

Vamos a empezar estudiando los "puntos notables" del triángulo: circuncentro, baricentro, incentro y ortocentro.

1-1 Mediatrices

La mediatriz de un segmento es la recta perpendicular al segmento que pasa por el punto medio. En el Cabri existe el comando perpendicular bisector, que traza la mediatriz de un segmento.

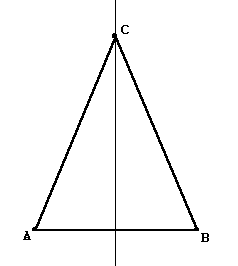
En la actividad 1.4 de la clase 0 vimos que todo punto en la mediatriz de un segmento forma con los vértices del segmento un triángulo isósceles. Es decir, AC = CB. Y por lo tanto también los ángulos CAB y CBA son congruentes. ¿Pudiste demostrar todas estas propiedades?

1-2 Mediatrices de un triángulo

1. Creá un triángulo ABC.
2. Trazá las mediatrices de los tres lados y mové la figura. ¿En cuántos puntos se cortan?

Sí, siempre se cortan en un punto. Esta es una propiedad muy importante de las mediatrices.

3. Demostrá esta propiedad. Sugerencia: usar la actividad anterior.
4. Marcá la intersección de las tres mediatrices y llamala O.
5. Mové los vértices del triángulo. Vas a ver que O está a veces afuera, a veces adentro del triángulo y a veces está sobre un lado. ¿Cuándo sucede cada caso?

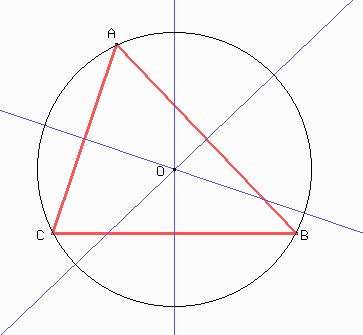
En preguntas como la que acabamos de hacer se ve cuánto nos ayuda el Cabri. Moviendo los vértices podemos intuir muy rápido la propiedad. En papel tendríamos que hacer muchas figuras para tener alguna sospecha.

1-3 El circuncentro

1. Trazá la circunferencia de centro O y que pase por un vértice. ¿Qué pasa?
2. ¿Te animás a decir por qué?

• El punto O se llama circuncentro y la circunferencia que trazaste es la circunscripta al triángulo.

Parte 2. Problemas

2.1 ¿Cuál es el circuncentro de un triángulo rectángulo?

2.2 Dado un cuadrilátero ABCD, ¿existirá siempre una circunferencia que pase por los cuatro vértices?

Todavía no estamos en condiciones de deducir qué propiedades tiene que cumplir un cuadrilátero para que exista la circunferencia circunscripta. Pero sí podemos resolver este problema:

2.3 Si el ángulo ABC de un cuadrilátero ABCD es recto y el cuadrilátero es circunscriptible (es decir, existe una circunferencia circunscripta al cuadrilátero), ¿cuánto mide el ángulo CDA?

Reciprocamente:

2.4 Si los ángulos ABC y CDA son rectos, ¿podemos afirmar que ABCD es circunscriptible?

2.5 Dados tres puntos A, B y O, construir un punto C tal que O sea el circuncentro de ABC y el área del triángulo ABC sea la mayor posible.

Así terminamos la tercera clase de EduCabr, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet Clase 4	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar