Clase 1 - Cuadrados

Esperamos sus mails en educabri@oma.org.ar.

 

Parte 1 - Actividades

1-1 Un cuadrado a partir de un lado

En la clase 0 les pedimos construir un cuadrado ABCD dado el lado AB. ¿Pudieron hacerlo?

Veamos una forma de hacerlo.

1. Creá un segmento AB.

Los puntos C y D del cuadrado estarán en las rectas perpendiculares a AB por los vértices de este segmento. Entonces, trazamos esas perpendiculares.

2. Trazá la recta perpendicular a AB que pase por A (perpendicular line).
3. Trazá la recta perpendicular a AB que pase por B (perpendicular line).

Ahora queremos encontrar los puntos C y D sobre las rectas que acabamos de trazar. Estos puntos tienen que cumplir AD = AB = BC. Podemos lograrlo usando circunferencias.

4. Trazá la circunferencia con centro en A que pase por B (circle by center & radius point).
5. Marcá la intersección entre esta circunferencia y la recta perpendicular por A. Este es el punto D.

Sólo nos falta C. Hay muchas posibilidades. Por ejemplo,

6. Trazá la recta paralela a AB por D.
7. Marcá la intersección entre esta recta y la recta perpendicular por B. Este es el punto C.
8. Oculta los objetos auxiliares para que quede sólo el cuadrado ABCD. (Cómo no se puede ocultar sólo un pedazo de recta, tendrás que ocultar toda las rectas y luego crear los segmentos que falten.)

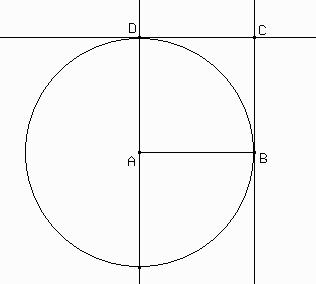
9. Respondé las siguientes preguntas:

1. ¿Qué otras formas se te ocurren para encontrar C?
2. ¿Qué pasa cuándo movés A o B?
3. ¿Qué pasa cuándo intentás mover D o C?
4. ¿Cómo harías un cuadrado en el que D y C se puedan mover pero A y B no?

1-2 Un cuadrado a partir de una diagonal

¿Qué pasa si queremos construir un cuadrado en el que A y C se puedan mover pero B y D no?

¡La construcción anterior no sirve!

Por eso, en la clase 0 otra actividad era construir un cuadrado dada la diagonal AC. Ahora hay formas muy distintas de hacerlo. Nos gustaría que nos cuentes cómo lo hiciste vos.

Parte 2. Problemas

2.1 Crear una circunferencia básica y colocar un punto P sobre ella.

1. Construir un cuadrado inscripto en la circunferencia, tal que uno de sus vértices sea P.
2. Construir un cuadrado circunscripto a la circunferencia, tal que P pertenezca a uno de los lados.
3. ¿Cuál es la razón entre las áreas de los dos cuadrados?

2.2 Construir un cuadrado ABCD y tomar un punto P en AB. Construir un cuadrado PQRS inscripto en el cuadrado ABCD.

2.3 En el problema anterior, construir un cuadrado EFGH inscripto en PQRS con lados paralelos a ABCD.

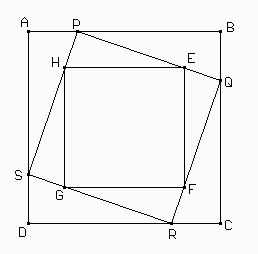
2.4 Dado un cuadrado ABCD y un punto P interior al cuadrado, construir un cuadrado EFGH, inscripto en ABCD tal que P pertenezca a uno de los lado de EFGH. (Este problema es de la prueba de selección argentina para la 4^a Olimpíada Matemática del Cono Sur y es bastante difícil.)

Esta fue la primer clase de EduCabir, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet  Clase 2	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar