Clase 13 - Problemas II

Esperamos sus mails en educabri@oma.org.ar.

Esperamos que les hayan salido los problemas que propusimos la clase pasada. Cualquier pregunta que tengan no duden en comunicarse con nosotros. Ahora, vayamos a los problemas de la clase de hoy.

Nivel Inicial

Dado un cuadrado ABCD de lado 1, sea P tal que CP = PD, CPD = 30° y P está más cerca de A que de C. Hallar la medida de AP.

Hagamos, primero la construcción de la figura. Empecemos por el triángulo CPD. Sabemos que CPD = 30° y como es isósceles, con CP = PD sabemos que PCD = PDC = (180° - 30°) / 2, es decir que miden 75°.

Para construir estos ángulos de 75° comencemos haciendo un triángulo equilátero sobre CD y luego tracemos las bisectrices como indica la figura.

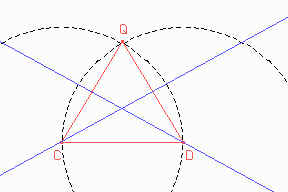
Estas bisectrices determinan con CD, ángulos de 30° ( la mitad de los ángulos de 60°). Para llegar a tener un ángulo de 75° debemos construir sobre estas bisectrices ángulos de 45°. Entonces trazamos las rectas perpendiculares a las bisectrices, y luego construimos las bisectrices estos ángulos de 90° que hicimos.

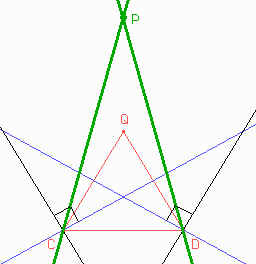
Lo único que falta, ahora, es construir el cuadrado sobre CD. Si no recuerdan como hacerlo puede ver la clase 1 del curso Educabri 1998. Veamos la figura terminada:

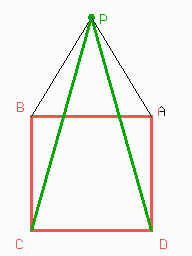
Como verán, el triángulo PAB es equilátero. Pero, ¿cómo lo demostramos? La idea acá, es usar un truco bastante conocido: partir de otra figura, más fácil de analizar, y demostrar que en realidad es la figura del enunciado.

Entonces tomemos la siguiente figura, formada por una cuadrado y un triángulo equilátero.

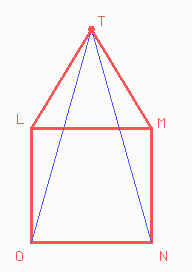Por, ahora, olvídense de la otra figura. Aquí partimos del cuadrado LMNO y el triángulo equilátero LMT. Entonces sabemos que TL = LM = TM por ser los lados de un triángulo equilátero y que LM = MN = NO = OL por ser los lados de un cuadrado. Por lo tanto, TL = LO. Además sabemos que: TLO = 60° + 90° = 150° Entonces por ser triángulo isósceles tenemos que LTO = LOT = (180° - 150°) / 2 = 15°. Del mismo modo probamos que MTN = 15°. Por lo tanto, OTN = 60° - 15° - 15° = 30°. Además, como los triángulos LOT y TMN son iguales tenemos que TO = TN. Es decir, esta figura es idéntica a la del problema y aquí sabemos que TM = MN !!! Entonces en la figura del problema AP = 1 que era el lado del cuadrado.

IMPORTANTE: Tengan en cuenta que aquí lo que hicimos fue tomar otra figura, definida con otras propiedades y luego demostrar que en realidad era la misma que la del enunciado pues cumplía con las propiedades que decía el problema. Una vez que demostramos que las dos construcciones son equivalentes y dan la misma figura, podemos extender las propiedades que se cumplen en una, a la otra.

Problemas y actividades

1. ¿Se les ocurre otra forma de resolver el problema? Prueben construyendo un triángulo equilátero sobre CD, interior al cuadrado.

2. Dado un cuadrado ABCD y un punto Q en su interior tal que QA = QB y AQB = 150°. Probar que CDQ es un triángulo equilátero.

3. Construir un triángulo tal que sus ángulos miden 75°, 45° y 60°.

El siguiente problema será tratado la clase próxima. Intenten resolverlo para la vez que viene así ya están en tema...

Dado un cuadrilátero convexo ABCD tal que el área de ABC es mayor que el área de ACD, trazar una recta que pase por A y que lo divida en dos partes de igual área.

Nivel Avanzado

Sean A y B dos puntos y C un punto cualquiera en el segmento AB. Sea D y E dos puntos del mismo lado del segmento AB tal que ADC = CEB = 120°, AD = CD y CE = EB. El punto F cumple que AF = BF, AFB = 120° y que F está en el semiplano determinado por AB que no contiene a D. Demostrar que DEF es un triángulo equilátero.

Este problema fue tomado este año en la prueba de selección para la Olimpíada del Cono Sur, en la que participan estudiantes menores de 15 años, de varios países de Sudamérica. El problema le trajo dificultades a bastante gente y por ese motivo decidimos tratarlo la clase de hoy.

La idea que subyace a este problema no es para nada complicada, una vez que uno la vió ...

Comencemos haciendo una figura de análisis. Confiamos en que sabrán construirla, solamente recuerden que cuando pongan C sobre AB, lo hagan con point on object porque es un punto cualquiera sobre el segmento.

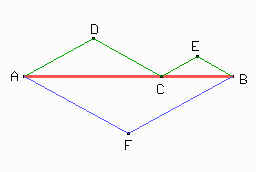
Esta figura es un poco complicada para probar que DEF es equilátero. En definitiva lo que queremos ver es que DE = DF = EF. Prolonguemos, entonces, las rectas CE y DC.

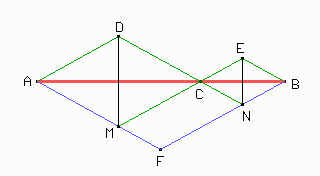
Si se fijan ADM es equilátero porque ADCM es un rombo y DAM = 60°. Del mismo modo probamos que ENB es equilátero.

Además sabemos que FN = AD por ser ADNF un paralelogramo y que MF = EB por ser EBFM un paralelogramo.

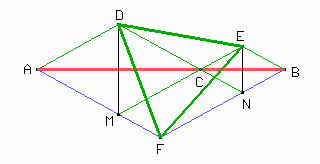
Entonces, veamos que los triángulos DMF, FNE y DCE son congruentes. Todos ellos tienen un lado igual a DM, pues DM = DC = FN y todos tienen un lado igual a EN pues EN = EC = MF. Además el ángulo comprendido entre estos lados en cada triángulo mide 120° pues es el suplementario del ángulo de 60° de los triángulos equiláteros.

Por lo tanto DE = DF = EF como queríamos probar.

Problemas y actividades

1. Sea ABCD un rectángulo y sea BCQ y CDP triángulos equiláteros exteriores al rectángulo. Demostrar que APQ es equilátero.

2. Si en el problema de la clase de hoy reemplazamos los ángulos de 120° por otro valor (todos iguales). ¿Es posible que DEF sea equilátero? ¿Es posible que DEF sea isósceles para toda posición de C?

El siguiente problema será tratado la clase próxima. Intenten resolverlo para la vez que viene así ya están en tema...

Sea K una circunferencia y sean A, B y C puntos sobre ella. Sea r la bisectriz de BAC, s la perpendicular a r que pasa por B y t la perpendicular a r que pasa por C. Sea P la intersección entre r y s. Sea Q la intersección entre r y t. Sea O el punto medio de PQ. Hallar el lugar geométrico de O a medida que A se mueve por K.

Será hasta la próxima. Hagan las actividades e intenten resolver los problemas. No se olviden de contestar la encuesta que se encuentra al final de la clase !!!

Esta fue la décimo tercera clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar