Clase 12 - Problemas I

Esperamos sus mails en educabri@oma.org.ar.

Luego de unas largas vacaciones volvemos con más Educabri. Introdujimos algunas modificaciones en la modalidad de las clases porque creemos que de esta forma las van a poder aprovechar mejor. Hasta ahora siempre tratamos temas teóricos y vimos la aplicación que tenían en diversos problemas.

Sin embargo quedaban algunas cuestiones sin tratar: aquellos problemas e ideas que utilizan varios temas teóricos a la vez. Es por este motivo que utilizaremos el mismo sistema que en los entrenamientos para las olimpíadas de matemáticas: resolver problemas. Los temas teóricos irán decantando solos a medida que solucionemos las situaciones planteadas.

Todas las clases veremos un problema de nivel inicial y uno de nivel avanzado que serán tomados de las Competencias de Clubes Cabri, de la Olimpíada Matemática Argentina y otras competencias. Además, ustedes podrán escribirnos proponiendo problemas para que se traten en clases posteriores.

Buenos, basta de charla y vayamos a los problemas de la clase de hoy ...

Nivel Inicial

Dados dos paralelogramos que no se superponen, trazar una recta que divida a ambos paralelogramos en dos figuras de igual área.

Concentrémonos en uno de los paralelogramos que llamaremos ABCD. La recta que debemos trazar debe dividir al paralelogramo en dos partes de igual área.

Sabemos que cada diagonal del ABCD lo divide en dos triángulos de igual área, de hecho los triángulos que quedan determinados son congruentes.

Si la recta, que llamaremos t, no corta a la diagonal AC entonces el paralelogramo quedará dividido en un pentágono y un triángulo que tiene menos de la mitad del área de ABCD.

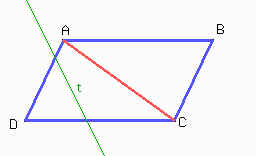
Entonces la recta t corta a la diagonal AC, pongamos en el punto P, y corta a dos lados del paralelogramo. Supongamos, sin perder generalidad que corta a AB y a CD en M y N respectivamente.

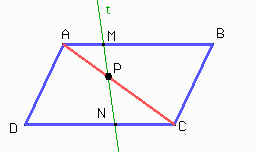
Como área(AMND) = 1/2 área(ABCD) = área(ACD) y además sabemos que:

área(AMND) = área (AMP) + área (APND)

área (ACD) = área (APND) + área (PNC)

Entonces igualando estas expresiones tenemos que área (AMP) = área (PNC). Dado que AB // CD, por ser ángulos alternos internos sabemos que MAP = PCN y AMP = PNC. Por lo tanto, los triángulos AMP y PCN son semejantes. Además de ser semejantes tienen igual área, entonces son congruentes, de donde deducimos que AP = PC.

Es decir, la recta t biseca a la diagonal AC. Del mismo modo, probamos que t biseca a BD. O sea, que t pasa necesariamente por la intersección de las diagonales de ABCD. Del mismo modo podemos probar que cualquier recta que pase por O divide al paralelogramo en dos cuadriláteros de igual área.

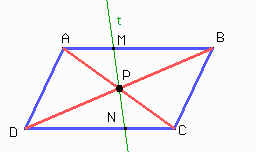
Por lo tanto, bastará trazar la recta que pase por los centros de los dos paralelogramos. Es más, esta recta será la única que cumple las propiedades del enunciado.

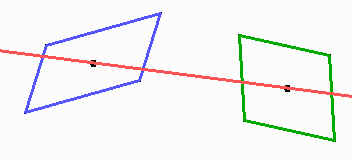
Problemas y actividades

1. En el problema, ¿era necesario que los paralelogramos no se superpusieran?

2. ¿Cuál es la condición necesaria para que la recta existiera y fuera única?

3. a) Construir un hexágono regular.
b) Probar que cualquier recta que pasa por el centro del hexágono lo divide en dos figuras de igual área.

El siguiente problema será tratado la clase próxima. Intenten resolverlo para la vez que viene así ya están en tema...

Dado un cuadrado ABCD de lado 1, sea P tal que CP = PD, CPD = 30° y P está más cerca de A que de C. Hallar la medida de AP.

Nivel Avanzado

Construir el triángulo ABC sabiendo que BAC = 60° y que el perímetro del triángulo es igual a 4 veces la altura desde A.

Este problema fue tomado en la segunda ronda de la 10ma Competencia de Clubes Cabri, en el nivel C, y decidimos tratarlo en esta primer clase de problemas por las dificultades que tuvieron los participantes al intentar resolverlo.

Parece bastante complicada la condición que la altura sea la cuarta parte del perímetro, y eso consideramos fue lo que más mareó a la gente.

La idea acá, es colocar los tres lados del triángulo sobre una recta y ver que podemos obtener de ello. Hagamos, entonces, una figura de análisis.

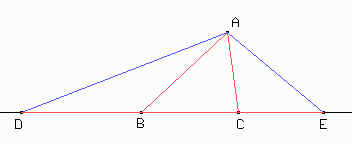
Sean D y E como se muestra en la figura tal que DB = AB y AC = CE. Calculemos la medida del ángulo DAE.

Como BAC + ABC + ACB = 180°, y BAC = 60° entonces sabemos que ABC + ACB = 120°. Por el otro lado, BDA = BAD = 1/2 ABC y CAE = CEA = 1/2 ACB. ¿Por qué?

Por lo tanto, BAD + CAE = (ABC + ACB) /2 = 60° de donde tenemos que DAE = 120°.

¿Cómo construimos, ahora, nuestro triángulo? Podemos comenzar con los puntos D y E sobre una recta. El punto A estará en el arco capaz de 120°. ¿Recuerdan que era el arco capaz? Es el lugar geométrico de todos los puntos A tal que los ángulos DAE miden lo mismo, en este caso 120°, y corresponde a un arco de circunferencia.

Para ello construimos un triángulo equilátero DEF, y trazamos la circunferencia circunscrita a DEF. Entonces los puntos P que estén en el arco DE que no contiene a F cumplirán que DPE mide 120°. Recuerden que en un cuadrilátero circunscriptible la suma de los ángulos opuestos es 180°.

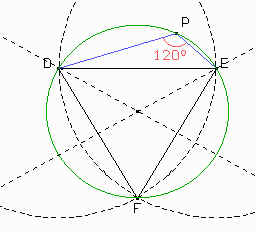
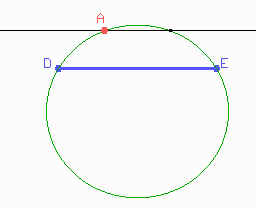
Ahora podemos hallar el punto A pues, como el perímetro de ABC es igual a DE entonces debemos trazar una recta paralela a DE tal que la distancia de dicha recta a DE sea la cuarta parte de DE. Les dejamos a ustedes la tarea de deducir como construirla a partir de la figura ...

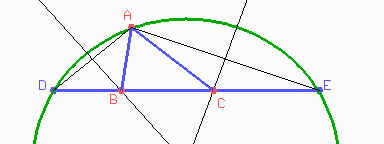
Una vez que encontramos A (elegimos uno de los dos, el otro nos da la figura simétrica) debemos hallar B y C. Para ello trazamos la mediatriz de AD que nos dará el punto B y la mediatriz de AE que nos dará el punto C.

Problemas y actividades

1. Construir un triángulo ABC que cumpla las siguientes condiciones:

• Si D es el pie de la altura desde A entonces 2(AB+BD) = 3(CD + CA)

• ABC = 30°

2. Construir un triángulo ABC tal que BCA = 30° y de modo que si M es el punto medio de BC entonces BC = AM.

El siguiente problema será tratado la clase próxima. Intenten resolverlo para la vez que viene así ya están en tema...

Sean A y B dos puntos y C un punto cualquiera en el segmento AB. Sea D y E dos puntos del mismo lado del segmento AB tal que ADC = CEB = 120°, AD = CD y CE = EB. El punto F cumple que AF = BF, AFB = 120° y que F está en el semiplano determinado por AB que no contiene a D. Demostrar que DEF es un triángulo equilátero.

Será hasta la próxima. Hagan las actividades e intenten resolver los problemas. No se olviden de contestar la encuesta que se encuentra al final de la clase !!!

Esta fue la décimo segunda clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar