Clase 11 - Competencias de Clubes Cabri - Nivel A

Esperamos sus mails en educabri@oma.org.ar.

 

En esta clase veremos las soluciones de los problemas que presentaron los distintos clubes en la 11^ma Competencia de Clubes Cabri. En caso de que aún no los hayan intentado resolver les sugerimos que lo hagan primero, antes de ver las soluciones que proponemos.

Problemas

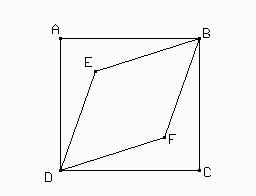
1. Construir la siguiente figura donde ABCD es un cuadrado y DEBF es un rombo cuya área es igual a la mitad del área del cuadrado.

2. Sea ABCD un trapecio con AB // CD tal que AB = AC = AD y BCD = 105°. Hallar los ángulos internos de ABCD y construirlo.

3. Sea ABCD un cuadrilátero tal que ADC = 45°, DCB = 90° y DAB = ABC. Sabiendo que la medida del lado CD es 1 hallar AD - BC.

4. ABC es un triángulo de perímetro 10 tal que la distancia de A a la recta BC es 3. Por A se traza una recta r paralela a BC. La bisectriz de B interseca a r en D y la bisectriz de C interseca a r en E. Hallar el área de BCDE.

5. Sea ABCD un trapecio isósceles con AB // CD y DA = AB = BC = 1 y DC = 2. Dividir la figura en 3 piezas de modo que se pueda armar con ellas, sin agujeros ni superposiciones, un triángulo equilátero. ¿Cuánto mide el lado del triángulo equilátero?

Soluciones

1. Como EBFD es un rombo entonces sus lados son iguales. Debido a que DE = EB y a que FB = DF tenemos que E y F están en la mediatriz de BD, al igual que lo están A y C. En otras palabras, E y F están sobre la diagonal AC del cuadrado.

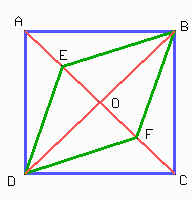
El área del rombo es igual a EF.BD/2 y el área del cuadrado es igual a AC.BD/2. ¿Recuerdan que el área de un rombo es igual a la mitad del producto de sus diagonales? Planteando, ahora, la razón entre áreas del enunciado llegamos a que EF.BD = AC.BD/2 por lo que 2.EF = AC.

Como DEBF es un rombo EO = OF (la diagonales de un rombo se bisecan perpendicularmente) de donde deducimos que E es el punto medio de AO y F es el punto medio de OC con lo que ya tenemos ubicados los puntos E y F.

Les dejamos a ustedes la tarea de hacer la construcción como ejercicio. Si no recuerdan como construir un cuadrado puede ver la Clase 1 de EduCabri 1998. Tengan en cuenta, como siempre, que para que la figura esté bien construida, al mover los puntos, no debe desarmarse y debe conservar todas las propiedades que pedía el enunciado.

2. Calculemos primero los ángulos para así poder luego construir la figura.

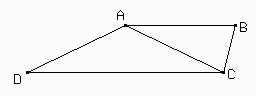
Si BAC = 2x entonces por ser ABC isósceles sabemos que ABC = ACB = 90° - x. Por el otro lado, como AB es paralelo a CD tenemos que ACD = BAC = 2x por ser alternos internos. Entonces BCD = 90° - x + 2x = 90° + x = 105°. Es decir que x = 15°.

Por ser ACD isósceles tenemos que 30° = ACD = ADC. Además ABC = 75° y finalmente obtenemos BAD = 360° - 75° - 105° - 30° = 150° pues la suma de los ángulos de un cuadrilátero es 360°. Hemos concluido, así, el cálculo de los ángulos del trapecio.

Construyamos ahora la figura. Para ello hagamos primero el triángulo ACD.

Tomamos un segmento CD y con centro en C y radio CD trazamos una circunferencia que se interseca con la circunferencia de centro D y radio CD en P. Por ser radios de una misma circunferencia PD = CD y PC = CD es decir que el triángulo CDP es equilátero.

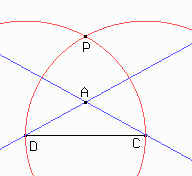
Las bisectrices de C y D se cortan en A de donde tenemos que CD = ADC = 30°. ¿Por qué? Nos falta entonces hallar el punto B.

Trazamos una recta paralela a CD que pase por A y luego la intersección de ésta con la circunferencia de centro A y radio AC nos da el punto B, por ser AB // CD y AB = AC.

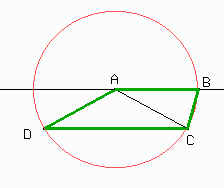
Hay otras formas de construir la figura, pero siempre debe conservar sus propiedades al mover los puntos de lugar. Es decir que no vale construir el cuadrilátero a ojo midiendo los ángulos y lados del mismo.

3. Al resolver éste problema es necesario prestar mucha atención a lo que pide el enunciado. Nos pide hallar la diferencia entre AD y BC para cualquier cuarilátero ABCD que cumpla con las condiciones dadas. No basta con con fijarse cuanto vale AD - BC para un caso particular; hay que hacer la demostración para el caso general. Bueno, ¡pongamos manos a la obra y a trabajar!

Para resolver este problema prolonguemos AD y BC que se intersecan en el punto E.

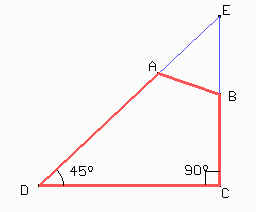
En el triángulo CDE el ángulo E = 180° - 90° - 45° = 45°. Por tanto el triángulo CDE es isósceles con CE = CD = 1. Además por el teorema de Pitágoras DE² = 1² + 1² de donde obtenemos que DE =.

Dado que DAB = ABC entonces sus suplementarios son iguales, es decir EAB = EBA. Con esto demostramos que EAB es isósceles, siendo EA = EB.

Entonces - 1 = ED - EC = (AD + EA) - (BC + EB) = AD - BC con lo que acabamos el problema. Fíjense que no importa cuánto midan los lados AD y BC la diferencia siempre será la misma.

4. En éste problema, igual que en el anterior, hay que hacer la demostración del caso general y no para algún triángulo con perímetro 10 y altura 3. Hagamos una figura de análisis para ver mejor qué se nos pide. Cabe destacar que la figura no respeta las condiciones del enuncido pues es sólamente una figura para fijar mejor los datos.

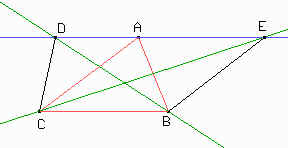
Por ser CE bisectriz del ángulo C sabemos que ACE = ECB. Además como AE es paralela a CB entonces AEC = ECB. Es decir que ACE = AEC, por lo que ACE es un triángulo isósceles con AC = AE.

Del mismo modo demostramos que ADB es isósceles con AD = AB.

Como DE // BC el cuadrilátero DEBC es un trapecio. Como recordarán el área de un trapecio es igual a la suma de sus bases multiplicado por la mitad de su altura.

Aquí la suma de las bases es ED + BC = DA + AE + BC = AB + AC + BC = 10. Y la altura, según el enunciado, era 3. Por tanto Área(DEBC) = 15.

5. Sean E y F los pies de las perpendiculares a CD desde A y B respectivamente.

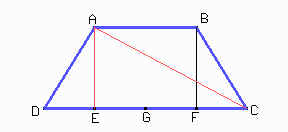
Como ABCD es un trapecio isósceles entonces DE = FC. Además EF = AB = 1 por lo que deducimos que DE = 0,5. Utilizando ahora el teorema de Pitágoras en el triángulo AED tenemos que AE = /2. Si G es el punto medio de EF entonces DG = 1 y además como AE es mediatriz de DG tenemos que AG = AD = 1 por lo que ADG es un triángulo equilátero.

Calculemos algunos ángulos para ver como podemos hacer la división. Por ser ADG equilátero tenemos que ADE = 60° y DAE = 30°. Como el trapecio es isósceles BCD = 60° por lo que ABC = BAD = 120°. El triángulo ABC es isósceles por lo que BAC = BCA = 30°.

EAC = 120 ° - 30° - 30° = 60° y entonces ECA = 30° por lo que EAC es medio triángulo equilátero. Si trasladamos el triángulo ADE y lo colocamos invertido de modo que AD coincida con BC (puede hacerse pues AD = BC y ADE + ABC = 180°) formamos la otra mitad del triángulo. Las piezas entonces se deben cortar de la siguiente manera:

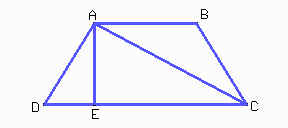
Y deben reordenarse de la siguiente forma para armar el triángulo equilátero:

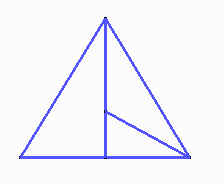
Nos falta todavía calcular el lado del triángulo. Para hacerlo basémonos en la primer figura que hicimos. En el triángulo AEC como EC = 1,5 utilizando el teorema de Pitágoras llegamos a que AC = que es la longitud del lado del triángulo equilátero formado.

Bueno, eso es todo por ahora. Recuerden responder la encuesta que está al final de la clase!!!

Esta fue la decimo primera clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar