
Clase 9 - Simetrías
Esperamos sus mails en educabri@oma.org.ar.
Clase 9 - Simetrías
Esperamos sus mails en educabri@oma.org.ar.
En esta clase utilizaremos las simetrías para mostrarles como ahorrar tiempo en las construcciones con el Cabri y también para mostrarles como usar esta idea en la resolución de problemas.
Al final de esta clase hay una encuesta que queremos que ustedes contesten. La idea es recibir opiniones del otro lado de la red, para saber que tal les están pareciendo las clases, los problemas que tratamos o si quieren sugerir algún tema para tratar en una futura clase. Así que cuando terminen de hacer esta clase, no se olviden de contestar la encuesta !!!
La idea de la simetría es muy simple: reflejar. Se puede hacer simetría con respecto a un punto o simetría con respecto a una recta. Veamos como es cada una.
Para hacer simetría con respecto a un punto, elegimos dos puntos, digamos A y O.
| El simétrico de A con respecto a O es un punto B de modo que O es el punto medio del segmento AB. |  |
En este caso, O se llama el centro de simetría. Pueden hacer esta construcción directamente con el comando Symmetrical Point del menú Construction. Primero deben señalar el punto que quieren simetrizar y después el centro de simetría.
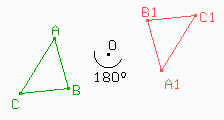
Para hacer la simetría de un triángulo ABC con respecto a un centro O, primero hay que encontrar los simétricos de A, B y C, y después unir; como se ve en el dibujo. Fíjense que la simetría con respecto a un punto, es lo mismo que un giro de 180° alrededor del centro de simetría. |
 |
Para hacer la simetría con respecto a una recta, elijan un punto A y una recta r.
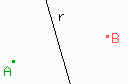 |
El simétrico de A con respecto a r es un punto B de modo que r es mediatriz del segmento AB. |
En este caso, r se llama el eje de simetría. Pueden hacer esta construcción directamente con el comando Symmetrical Point del menú Construction. Primero deben señalar el punto que quieren simetrizar y después el eje de simetría.
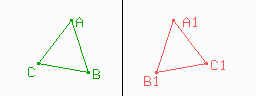
| Para hacer la simetría de un triángulo, igual que
en la simetría con respecto a un punto; hay que hallar
primero los simétricos de los vértices y luego unir. Observen que la simetría con respecto a una recta, es como mirar la figura a través de un espejo. |
 |
| Para fijar ideas, usemos la simetría para construir la siguiente figura. | 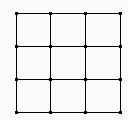 |
Lo que a uno primero se le ocurre; es hacer un cuadrado grande y después dividir cada lado en tres partes iguales. Bueno, la idea no es mala; pero el único problema es que dividir el lado en tres partes iguales no es fácil. Si te sale, ¡genial!, pero si no, hay que buscar otra forma.
Aquí veremos como hacer la construcción desde el cuadrado chiquito, si quieren ver como se divide un segmento en tres partes para hacerlo con el cuadrado grande pueden ir a la clase 19 del curso Educabri 98.
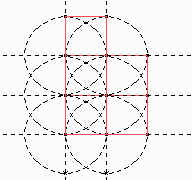
Empecemos por un cuadrado chiquito. Construir un cuadrado es fácil, y después podríamos empezar a construir los restantes 8 cuadraditos sobre los lados que ya tenemos; de esta manera. Nosotros, en la figura, empezamos esta construcción; pero como se ve, hay demasiadas rectas y circunferencias. ¡Y eso que recién construimos 5 de los 9 cuadraditos que hay que hacer! Debe haber una forma mejor. |
 |
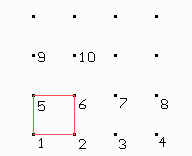 |
Una forma más fácil es hacer el primer cuadrado (1265) y el resto de los puntos obtenerlos usando Symmetrical point, de modo que 3 es el simétrico de 1 con respecto a 2, 4 es el simétrico de 2 con respecto a 3, 9 es el simétrico de 1 con respecto a 5, 10 es el simétrico de 2 con respecto a 6, y así sucesivamente ... después sólo quedan por marcar los segmentos ¡y listo! |
Ahora les dejamos algunos problemas para que practiquen lo aprendido.
Problemas
1. Construir un rectángulo donde un lado mida el doble del otro. Tengan en cuenta que la figura no se debe desarmar al mover los puntos.
2. Construir un trapecio isósceles ABCD con AB // CD de modo que AB = 1, BC = 2 y CD = 3.
3. Dadas dos rectas r y s, que no sean paralelas, y un punto P que no pertenezca a ninguna de las dos, se traza el simétrico de P con respecto a r, llamémoslo Q. El simétrico de Q con respecto a s se llama R y el simétrico de R con respecto a r se llama S. Demostrar que P, Q, R y S están sobre una circunferencia.
Así terminamos la novena clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.
Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
.
|