Certamen Zonal
Primer nivel

1. ¿Cuántos números naturales de 4 cifras terminan en 36 y son múltiplos de 36?

2. En el romboide ABCD las diagonales se cortan en el punto F (los lados iguales son AB = BC y CD = DA). Sobre la prolongación del lado BC se marca un punto E de modo que CF = CE y el cuadrilátero FCED es romboide. ¿Si ABC = 122 grados, cuanto mide el ángulo ADE?

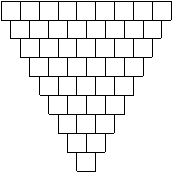
3. Colocar en cada casilla vacía un dígito distinto de cero de modo tal que a partir de la segunda fila, el número de cada casilla sea igual a la resta de los dos números ubicados en las casillas vecinas de la fila anterior.

Segundo nivel

1. Empezando con 46, se forma una secuencia de dígitos colocando, en cada paso, a continuación del ultimo número escrito, el producto de los dos últimos dígitos que se escribieron (los primeros 5 dígitos son: 46248...).

Calcular el dígito que esta en la posición 1996.

2. Sea t una recta y P un punto exterior. Sobre la recta se marcan de izquierda a derecha los puntos A, B, C, D, E de modo que PA=PB, PB=BC, PC=CD y PD=DE. Se traza por P la paralela a t y se marca en esta paralela el punto Q tal que PQED es un paralelogramo.

Si los ángulos QED y APB son iguales, ¿cuánto mide el ángulo PAB?

3. El druida Panoramix desea preparar 24 cucharones de una pócima mágica que contenga las sustancias A, B, C por partes iguales. Dispone de un recipiente donde hay A y C mezclados por partes iguales; otro en el que hay A y B mezclados en la proporción 2:3 y un tercero en el que hay B y C mezclados en la proporción 1:2. ¿Cuántos cucharones de cada recipiente debe mezclar para obtener la pócima deseada?

NOTA: las cantidades X e Y están en proporción 2:3 si X/Y=2/3.

Tercer nivel

1. Colocar números naturales distintos y mayores que 1 en las casillas de manera que siempre el número de una casilla sea múltiplo del que esta en la casilla anterior y que la suma de los cinco números sea 517.

2. Una hormiga parte del hormiguero y recorre en línea recta un tramo de d cm, luego gira 90o y recorre en línea recta otro tramo de d/2 cm, luego vuelve a girar 90o y recorre un tramo de d/(22) cm, y así sucesivamente. El sentido en que gira lo decide en cada vértice.

¿Cuál es la menor distancia al hormiguero a la que puede estar la hormiga después de haber recorrido 100 tramos?

3. Encontrar TODAS las ternas de números reales (x,y,z) que verifican simultáneamente:

x2 + y + z = 1

x + y2 + z = 1

x + y + z2 = 1

[ Certamen Regional ]

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar