XII Olimpíada Matemática Argentina. 1995

Certamen Regional

 

Primer nivel

1. Verónica y su amigo Julio entraron a una librería de Bahía Blanca y compraron por valores enteros diferentes, superiores a $10. Cada uno quiso pagar con un billete de $20, pero el dueño no tenía cambio para cobrarle a ninguno de los dos. Entonces Julio ofreció pagarle con un billete de $50 y así pudo darle el vuelto. Al ver esto, Verónica sacó un billete de $50 y el librero pudo cobrarle a ella también. ¿Cuál es el número mínimo de billetes que podía tener el librero cuando llegaron los amigos?
NOTA: Los billetes en circulación son de $100, $50, $20, $10, $5, $2, $1.

2. Escribir en cada vértice de un cuadrado una potencia de 2 y luego, en cada lado y en cada diagonal escribir el producto de los números asignados a sus extremos, de modo tal que la suma de los 10 números escritos sea 3505.
ACLARACION: Las potencias de 2 son 20=1, 21=2, 22=4, ...

3. En una circunferencia de centro O y radio 1 se marcan los puntos A, B, C y D siguiendo el sentido horario. Si AOB=120o, BOC=60o y COD=150o, calcular el área del cuadrilátero ABCD.

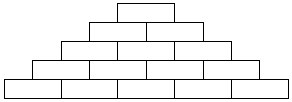
Segundo nivel

1. Escribir en cada casilla de la pirámide un número natural mayor que 1 de modo que:

piramide (5 casillas de base - 5 casillas de altura)

2. Cuatro autos A, B, C y D salen simultáneamente de un mismo punto de una pista circular. A y B van en una dirección, C y D en la dirección contraria. Todos tienen distintas velocidades, pero constantes. A los 5 minutos de la partida, A cruza por primera vez a C y en el mismo instante, B cruza por primera vez a D. A los 83 minutos de la partida, A y B se encuentran por primera vez. ¿Cuánto tiempo transcurre desde la partida hasta que C y D se encuentran por primera vez?

3. Dada una circunferencia C de centro O y una circunferencia C' que pasa por O y corta a C en A y B, sea C (distinto de O) un punto de C' que está en el interior de la circunferencia C. La recta AC corta nuevamente a la circunferencia C en D. Demostrar que CB=CD.

Tercer nivel

1. Tomando como vértices los puntos de intersección de las prolongaciones de los lados de un hexágono regular H0 se obiene un nuevo hexágono regular H1. De la misma manera, a partir de H1 se construye H2 y así sucesivamente. ¿Cuál es el primer hexágono Hn cuya área es mayor que 1995 veces el área del hexágono H0?

2. Consideramos los números enteros de 1 a 1000 inclusive. Sumamos entre sí todos los que tienen todos sus dígitos pares y sumamos entre sí todos los que tienen todos sus dígitos impares. ¿Cuál suma es mayor?

ACLARACION: 0 es par.

3. Dados tres puntos no alineados A, B, C, construir una circunferencia con centro en C tal que una de las tangentes trazadas desde A sea paralela a una de las tangentes trazadas desde B. Indicar los pasos de la construcción.

Certamen Zonal

 

Archivo de Enunciados Página Principal Olimpíada Matemática Argentina
   www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar

 

duty free alcohol duty free cigarette online cigars duty free where to buy cosmetics online duty free fragrances prices buy duty free tobacco uk
dy>