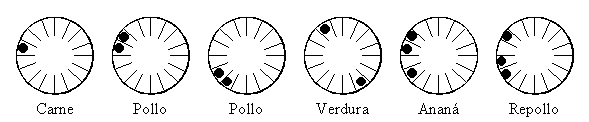
¿Cuántos gustos diferentes puede haber, de manera que por la posición de los agujeritos se pueda distinguir de qué gusto son?
(Nota: La tapa de arriba de las tartitas se pinta con huevo.)
2º Torneo de Computación y Matemática
Tercera Ronda
11 de noviembre de 1999
Nivel 1 (7mo y 8vo año de escolaridad)
1
Pablito tenía 5040 soldaditos, pero se le perdieron algunos. Si intenta separarlos en grupitos de a 7 le sobran 3. Cuando trata de formarlos en fila, de a 12 por fila, le sobran 5. Al intentar armar equipos de 10 integrantes le sobra 1 soldadito. Si intentara armar grupitos de a 13 le sobrarían 12. ¿Cuántos soldaditos se le perdieron?
2
La abuela de Danielito le regala plata cada mes. El primer mes le regaló $2, el segundo $3, el tercero $5, el cuarto $7, el quinto $11, y así sucesivamente, cada mes el primo siguiente. Como es muy precavido, ahorró todo este dinero y justo este mes superó los $10.000. ¿Cuánto dinero le regaló su abuela?
3
Se toman los múltiplos de 7,
entre 1 y 10000. Calcular el resultado de sumar la cifra de las
decenas de dichos números.
(Nota: la cifra de las decenas de 1428 es 2.)
Nivel 2 (9no y 10mo año de escolaridad)
1
¿Cuál es el mayor primo que divide a 332 - 1 ?
2
En la rotisería "El Repulgue
Feliz" cocinan muchos gustos diferentes de tartitas. Cada
tartita tiene forma de disco, pero como son muy parecidas, se les
hacen agujeritos para que los compradores puedan distinguir los
diferentes gustos. Hay 16 lugares para hacer agujeritos en el
borde. Por ejemplo las de carne tienen un agujerito, las de pollo
dos agujeros consecutivos, las de verdura dos agujeritos en
posiciones opuestas, las da ananá y las de repollo tienen tres
agujeritos en distinta posición como se ve en la figura, etc.
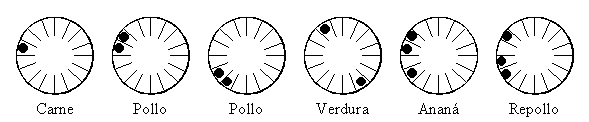
¿Cuántos gustos diferentes
puede haber, de manera que por la posición de los agujeritos se
pueda distinguir de qué gusto son?
(Nota: La tapa de arriba de las tartitas se pinta con huevo.)
3
Una máquina calcula números de
Fibonacci, pero comete errores de cálculo: en algunos pasos
calcula correctamente F(k+2) = F(k+1) + F(k), pero en otros pasos
calcula F(k+2) = | F(k+1) - F(k) |. (Nota: |x| es el valor
absoluto de x, por ejemplo |4| = 4; |-7| = 7 )
Se pueden ingresar por el teclado 3 números enteros positivos a,
b y n (n mayor o igual que 3). La maquina asigna F(1) = a, F(2) =
b, calcula "F(n)" (efectuando pasos a veces correctos y
a veces erróneos) y lo imprime. Por ejemplo si uno ingresa a =
2; b = 9; n = 7. La computadora podría imprimir 38 (calculando 2
-> 9 -> 11 -> 20 => 9 -> 29 -> 38) o también 2
(2 -> 9 => 7 => 2 => 5 => 3 => 2) o también 2
(2 -> 9 -> 11 => 2 -> 13 -> 15 => 2) o también
82 (2 -> 9 -> 11 -> 20 -> 31 -> 51 -> 82) o
muchos otros resultados más.
Encontrar a, b y n para que todos los "F(n)" que la
máquina puede llegar a imprimir sean exactamente:
1; 3; 5; 7; 9; 11; 13; 15; 17; 19; 21; 23; 27; 29; 31; 33; 35;
37; 39; 41; 43; 45; 47; 49; 51; 53; 55; 57; 59; 61; 63; 65; 67;
71; 73; 77; 79; 83; 87; 89; 91; 95; 115; 119; 121; 131; 157; 167;
169; 173; 199; 377 .
Nivel 3 (11er año de escolaridad en adelante)
1
Calcular con por lo menos 10
cifras decimales correctas
![]()
en donde pn es el n-ésimo número primo. Por ejemplo p1=2,
p6=13, p7=17 .
2
¿Existe algún n entero positivo
compuesto que divida a 2n-1 - 1 ? Justificar que no
existe o encontrar el mínimo n que cumple.
(Nota: 1 no es compuesto.)
3
Decidir si es posible llenar los casilleros de un tablero cuadrado de 4 por 4 con los siguientes números (sin repetir), de manera que los cuatro números de cada fila y los cuatro números de cada columna sumen lo mismo.
7; 21; 34; 48; 51;
54; 58; 61; 64; 77; 108; 111; 138; 194; 197; 217
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |