Primer
Torneo de Computación y Matemática
Ronda Final
Diciembre de 1998
Nivel 1 (7mo y 8vo
año de escolaridad)
1
Encontrar 4 números enteros, todos mayores
que 1, tal que se cumple que el mínimo común múltiplo entre
todos ellos es 486529981 veces el máximo común divisor entre
todos ellos.
2
Contar cuántas ternas (x,y,z) de números
enteros positivos verifican que la suma de sus cuadrados da 19982.
Aclaración: La terna (264,552,1902) no es igual a la terna
(264,1902,552).
3
Contar cuántos múltiplos enteros
positivos hay del número 3333 con la propiedad de que ninguno de
sus dígitos se repite, y ningún dígito es igual a cero.
Nivel 2
(9no y
10mo año de escolaridad)
1
Calcular la probabilidad de sumar 35
tirando 10 dados.
Aclaración: La probabilidad es igual al
número de casos favorables dividido por el número de casos
posibles. Por ejemplo, la probabilidad de que salga 3 tirando un
dado es 1/6.
2
Se toma un número entero positivo N. Se
suman sus dígitos. Se vuelven a sumar los dígitos de este
resultado. Este procedimiento se aplica sucesivamente hasta
obtener un número de un solo dígito, que se llama la suma
estacionaria de los dígitos de N (ej. 1998 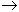 27
27 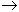 9).
9).
Análogamente, multiplicando los dígitos de N, multiplicando los
dígitos del resultado de esta operación y aplicando
sucesivamente este procedimiento hasta llegar a un número de un
solo dígito, se obtiene el producto estacionario de los
dígitos de N (ej. 1998 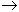 648
648 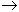 192
192 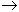 18
18 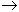 8).
8).
Contar cuántos números enteros positivos hay, menores o iguales
que 19982, que tienen la misma suma y producto
estacionarios.
3
Distribuir 21 números enteros
distintos entre 0 y 25 (ambos inclusive) en las circunferencias
de la siguiente figura de tal manera que la suma de los vértices
de cada triángulo sombreado sea siempre la misma.
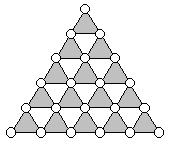
Nivel 3 (11er año de
escolaridad en adelante)
1
Contar de cuántas maneras distintas puede
cubrirse un tablero de 3x28 usando fichas de dominó (2x1).
Aclaración: El tablero se considera fijo, es decir,
rotaciones y simetrías se consideran distintas formas.
2
Una hormiguita viaja sobre un rayo de la
rueda trasera de la bicicleta de Martín, caminando desde el
borde hacia el centro con velocidad constante. Estimar la
longitud de la trayectoria que describe la hormiguita desde que
se sube a la rueda hasta que llega al centro, sabiendo que lo
hace en el mismo tiempo en que la rueda da una vuelta y que la
rueda tiene radio 1. Se pide la respuesta con una precisión de
por lo menos 2 dígitos.
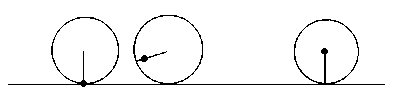
3
- Contar cuántas potencias de 5 hay
tales que la suma de sus dígitos es menor que 20.
- Contar cuántas potencias de 5 hay
tales que la suma de sus dígitos es menor que 45.