- f (0)=0
- f (1)=1
- si n
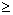 2 entonces f (n)
= f (n-1) + f (n-2)
2 entonces f (n)
= f (n-1) + f (n-2)
Primer
Torneo de Computación y Matemática
2da Ronda
16 de Octubre de 1998
Nivel 1 (7mo y 8vo año de escolaridad)
1
Encontrar todos los pares (x , y) de enteros positivos que verifican x2 + 3xy + y3 = 947139.
2
¿Cuántos de los primos menores que 10000 se pueden expresar como suma de dos primos? (nota: 0 y 1 no son primos)
3
¿Cuántos números capicúas de 8 cifras son cuadrados perfectos? (por ejemplo 289=172 es un cuadrado perfecto)
Nivel 2 (9no y 10mo año de escolaridad)
1
¿Cuál es la primera potencia de 2 que
tiene tres ceros consecutivos en su escritura decimal?
(Por ejemplo 224=16777216 tiene tres sietes
consecutivos)
2
Se dice que un primo impar p es un casi-divisor de n si al dividir n por p se obtiene resto (p-1)/2 (2 no es casi-divisor de nadie). ¿Cuántos números menores a 10000 hay que tienen exactamente dos casi-divisores primos distintos?
3
La sucesión de Fibonacci se define de la siguiente manera:
- f (0)=0
- f (1)=1
- si n
2 entonces f (n) = f (n-1) + f (n-2)
(o sea f (2)=1 ; f (3)=2 ; f (4)=3 ; f (5)=5 ; f (6)=8;... )
Calcular a primera y la última cifra de f
(1998).
(Nota: La primera cifra de 3482 es 3 y la ultima es 2)
Nivel 3 (11er año de escolaridad en adelante)
1
Calcular cuántos números enteros de 10
cifras hay tales que cada una de sus cifras es 1, 2 o 3 y no hay
cuatro cifras consecutivas iguales.
Por ejemplo: 12312311, 1112223331, 1212121212, 3212233311, etc.
2
¿Es primo el número formado al escribir en forma consecutiva todos los primos menores que 10000 (o sea 23571113... )? Justificar.
3
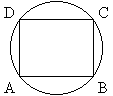
Se tiene un ABCD rectángulo inscripto en un circulo de radio 1. ¿Cuáles deben ser los lados del rectángulo para que la longitud del lado AB, sea igual a la longitud del arco BC.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |