Primer Torneo de Computación y Matemática
1era Ronda

14 al 21 de Agosto de 1998

Nivel 1 (7^mo y 8^vo año de escolaridad)

1

Contar cuántos números primos positivos hay menores o iguales que 1.000.000.000 tal que el producto de sus dígitos también es un número primo.
(Aclaración, ni 0 ni 1 son números primos).

2

Fui a comprar 127 paquetes de pastillas al kiosco de la esquina, pero solo tenía billetes de $1000. Le di varios de ellos al kiosquero y él me devolvió $40 de vuelto. ¿Cuál es la menor cantidad de billetes que pude haberle dado?

3

Encontrar todos los números enteros positivos n menores o iguales que 26.270 que verifican que n²+1 es un número primo.

Nivel 2 (9^no y 10^mo año de escolaridad)

1

Listar 10 primos positivos en progresión aritmética.
(Aclaración: una lista de números está en progresión aritmética si la diferencia entre dos consecutivos es constante.)

2

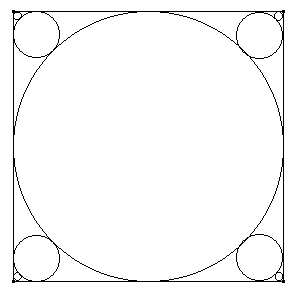
Se inscribe una circunferencia en un cuadrado de área 1. Luego, se inscriben 4 circunferencias en cada una de las esquinas. Se realiza este procedimiento (inscribir 4 circunferencias en cada una de las esquinas) 999.999 veces más. Calcular el área de la figura que resulta de sombrear todas las circunferencias.

3

Daniel tiene muchas monedas de 5, 10, 25 y 50 centavos y también de 1 peso. Quiere comprarse un mouse que cuesta $5,50. ¿Con cuántas combinaciones distintas de monedas puede pagar el precio exacto del mouse?

Nivel 3 (11^er año de escolaridad en adelante)

1

Se toma un número entero positivo, se le suma 5141 y después se divide el resultado de la suma por el primo más grande que divide a esa suma. Demostrar que comenzando con cualquier número entero e iterando esta operación, siempre se termina en 1.

2

En una jaula se desean colocar 3 especies de ratas: blancas, negras y marrones. Se sabe que si en algún momento hay mas ratas de alguna especie que la suma de las otras dos, entonces el grupo mayoritario atacará a las otras especies, por lo tanto esto nunca debe suceder. Se van a colocar 5 ejemplares de cada especie, y se introducirán en la jaula de a uno por vez. ¿De cuántas maneras es posible hacer esto?

3

Se tienen la circunferencia con centro en (0,0) y radio 1, y una elipse con el mismo centro y la misma superficie. ¿Cuáles deben ser los radios de la elipse para que el área en la intersección de la circunferencia con la elipse sea igual a la suma de las áreas de las 4 regiones que quedan fuera de dicha intersección? Se pide la respuesta con una precisión de 4 decimales.

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar