Torneo Computación y Matemática
Problemas de entrenamiento Serie 1

Nivel 1 (7^mo y 8^vo año de escolaridad)

1

Contar todos los números de 5 dígitos tales que la suma de sus dígitos es un número primo.

2

Calcular cuántos pares ordenados (a,b) de números enteros verifican 1998<a²+b²<1998².

3

Calcular cuántas son todas las ternas de números primos (p₁, p₂, p₃) tales que cada uno de ellos es menor o igual que 50, y es posible construir un triángulo con longitudes p₁, p₂ y p₃.

Nivel 2 (9^no y 10^mo año de escolaridad)

1

Calcular todos los pares de números racionales (a,b) que verifican a²+b²=1, y que se puedan escribir como fracción irreducible con denominador de hasta 2 dígitos.

2

Calcular los dos últimos dígitos de

1¹+1²+...+1¹⁹⁹⁸+2¹+2²+...+2¹⁹⁹⁸+...+1998¹+1998²+...+1998¹⁹⁹⁸.

3

La sucesión aleatoria de Fibonacci se construye de la siguiente manera: los dos primeros términos valen 0, 1. Para calcular del tercero en adelante, se tira una moneda: si sale cara, se restan los dos términos anteriores (si no son iguales, el mayor menos el menor); si sale seca, se suman. Calcular cuántos valores distintos puede asumir el término que ocupa el lugar 15.

Nivel 3 (11^er año de escolaridad en adelante)

1

Encontrar el menor entero a para el cual la ecuación x⁴-36x³+x²+a = 0 NO tenga soluciones reales.

2

En Truchilandia solo hay billetes de 3, 5 y 8 truchipesos. Determinar todos los precios que NO es posible pagar justo sin recibir vuelto en ese país.

3

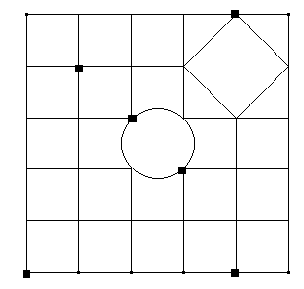
El profesor de Instrucción Cívica desea que sus alumnos conozcan el barrio. Para ello, debe salir de la escuela que se encuentra en el vértice inferior izquierdo del mapa, y planea pasar por los 5 puntos marcados en el mismo. Indicar un camino que minimice la distancia del recorrido. Tener en cuenta que el paseo termina retornando nuevamente a la escuela.

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar