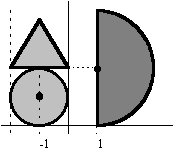
PreTorneo de Computación y Matemática
Olimpíada Matemática Rioplatense, 1997
Único Nivel
1
Contar cuántas maneras distintas hay de pintar un cubo, usando hasta 4 colores de tal manera que dos caras adyacentes reciban colores distintos.
(Aclaración: dos coloraciones son distintas si no hay ninguna rotación del cubo que transforma una en la otra.)
2
Se define f(n) como la cantidad de formas distintas en que puede escribirse a n como suma de enteros positivos (sin importar en que orden se sumen, por ejemplo 15 = 7 + 3 + 5 y 15 = 5 + 3 + 7 se consideran la misma forma). Calcular f(120).
3
La figura F1 está compuesta por un círculo y un triángulo equilátero. La figura F2 es un semicírculo. La recta y=ax+b divide a cada una de las figuras en partes de igual área. Encontrar los valores de a y b con una aproximación de tres decimales.
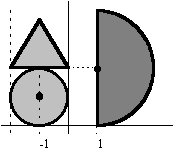
4
El número 100...001 tiene n
dígitos y es primo. Calcular los valores de 2 
n 50
para los cuales esto ocurre.
 Archivo de Enunciados CyM Página Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |