con a, b, c, d enteros
no negativos y a+b+c+d 
100. Calcular 
10 S![_]](cym_rpe.gif){kind=small}
.Aclaración:
x es la parte entera de
x, y n! = 1·2·3·..·n (ejemplo:3.2=3, 4=4 , 5.71=5, 5!=120)4to
Torneo de Computación y Matemática
Ronda
Final
Villa Carlos Paz, 16 al 19 de diciembre de 2001
Nivel 1 (7mo y 8vo año de escolaridad)
Primer día
1
Hallar a y b enteros positivos tales que a·b·2291-889·b2 sea primo. Dar 5 ejemplos.
2
Encontrar el valor de las cifras a, b, c de manera que al multiplicarse los tres números de tres cifras "abc", "bca" y "cab" se obtenga como resultado 113197392 .
3
a) Contar cuántas duplas de números
enteros positivos (x;y) verifican la igualdad x2+y2=27625
b) Contar cuántas duplas de números enteros positivos (x;y)
verifican la igualdad x2+y2=260365625
Segundo día
4
¿Cuántos números de 4 cifras, todas distintas de cero y diferentes entre si, son divisibles por el producto de sus dígitos?. Por ejemplo: 1296.
5
La empresa Exeq vende 3 modelos de computadoras: el modelo Hogar, que cuesta $1234; el modelo Profesional, a $1991; y el modelo Empresario, que cuesta $2345. El último mes vendieron 2001 unidades en total, recaudando $4321234. Decir cuántas unidades vendieron de cada modelo. ¿Es la única posibilidad?
6
a) Blas escribe en un pizarrón todos los
múltiplos de 37 menores que 30000. Luego toma la última cifra
de cada número y borra todas las otras. Calcular la suma de los
números que quedaron escritos en el pizarrón.
Aclaración: La última cifra de 207 es 7, de 4 es 4, de 12131 es
1, de 3420 es 0.
b) Juan escribe en un pizarrón todos los
múltiplos de 37 menores que 30000. Luego toma la primera cifra
de cada número y borra todas las otras. Calcular la suma de los
números que quedaron escritos en el pizarrón.
Aclaración: La primera cifra de 207 es 2, de 4 es 4, de 12131 es
1, de 3420 es 3.
Nivel 2 (9no y 10mo año de escolaridad)
Primer día
1
Durante un largo viaje, Alejandro escribe los cuadrados de los números naturales, desde 1 hasta el de 2001, o sea 1, 4, 9, ..., 4000000, 4004001 ¿Cuántas veces aparece escrita la cifra 7?
2
Contar todos los divisores de 479001600 (=12!) que se pueden escribir de la forma 2a2+b3, con a y b enteros positivos.
3
Se escribe el número N concatenando todos
los enteros desde 4973 hasta 5026, o sea
N=4973497449754976..502450255026. Decidir si N es múltiplo de:
a) 3
b) 11
c) 121
d) 2001
e) 159178
f) 159179
Segundo día
4
Sea S la suma de todos los números de la
forma con a, b, c, d enteros
no negativos y a+b+c+d 100. Calcular 10 S.
Aclaración: x es la parte entera de
x, y n! = 1·2·3·..·n (ejemplo:3.2=3, 4=4 , 5.71=5, 5!=120)
5
Encontrar el menor entero positivo N tal
que la suma de los divisores de N sea mayor o igual a:
a) 4·N.
b) 4,5·N.
Aclaración: los divisores de 60 son
1,2,3,4,5,6,10,12,15,20,30,60
6
Buscar todas las ternas de números enteros positivos (x;y;z) que verifican que 5(x+y+z)=xyz
Nivel 3 (11er año de escolaridad en adelante)
Primer día
1
Reemplazar los signos "?" de la
siguiente expresión por signos "+" y "*" de
manera que se verifique la igualdad:
1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7 ? 8 ? 9 = 134
Aclaración: tener en cuenta la precedencia de * respecto a +.
Por ejemplo 3 + 7*4 + 1= 32.
2
Encontrar el menor entero positivo que
tenga exactamente:
a) 400 divisores.
b) 1000 divisores.
3
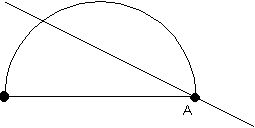
Dada una semicircunferencia, se traza una recta que pasa por A (uno de los vértices, extremo del diámetro) y divide a la semicircunferencia en dos partes. ¿Qué ángulo debe formar la recta con la base para que las partes tengan la misma área?
a) Calcular el resultado con un error menor
que 0,001
b) Calcular el resultado con un error menor que 0,00000001
Segundo día
4
Una cadena de primos a derecha es
una secuencia de números enteros positivos que son todos primos,
el primero tiene una cifra, y cada uno de los demás se obtiene
de su predecesor agregando una cifra a la derecha, por ejemplo 3 
31 313 3137 31379, que tiene largo 5.
Hallar una cadena de primos a derecha tal que no haya ninguna
otra cadena de primos a derecha de longitud mayor.
5
Leandro y Pablo juegan el siguiente juego.
Se fija un número N de antemano. Alternativamente, uno de ellos
dice un número capicúa A, y el otro busca dos números B, C,
también capicúas, tal que N = A + B + C. Por ejemplo 81796 =
1+77+ 81718. El que se equivoca pierde.
Pregunta: ¿De cuántas formas se puede escribir 90266132 como
suma de tres números capicúa?
Nota: "1+77+ 81718" y "81718 +1+77" son la
misma forma de escribir 81796, mientras que "1+77+
81718" y "72127+3333+6336" son dos formas
distintas.
6
Se dibujan n-3 diagonales en un polígono convexo de n lados, de manera que no se corten. La figura obtenida es una triangulación del polígono.
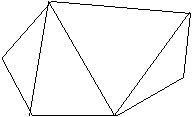
¿Cuántas triangulaciones tiene un polígono convexo de 21 lados?
 Archivo de Enunciados CyM Página Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |