3^er Torneo de Computación y Matemática
Primera Ronda

29 de agosto al 5 de septiembre de 2000

Nivel 1 (7^mo y 8^vo año de escolaridad)

1

Encontrar cuatro números enteros positivos a, b, c, d tales que (a³+b³)/(c³+d³)=1/2000 .

(Nota: cero no es un número entero positivo.)

2

Una acaudalada anciana tiene gran cantidad de lingotes de oro de tres tipos: por valor de $56, de $106, y de $127. ¿Cuál es la menor cantidad de lingotes que puede usar para depositar exactamente $5409 en una caja de seguridad de un banco?

3

¿Cuántos divisores primos distintos tiene 1279224 ?

(Nota: Un número es primo si solamente se puede dividir por el número uno y por sí mismo. Por ejemplo 2 ,3 ,5 ,7, 11, 13, 17, 19, ... )

Nivel 2 (9^no y 10^mo año de escolaridad)

1

Encontrar todos los números de tres cifras n tales que el número que se obtiene al dar vuelta las cifras de n² es un múltiplo de n.

(Nota: Al dar vuelta las cifras de 1453 se obtiene 3541 .)

2

¿Cuál o cuáles son los números enteros positivos entre 1 y 10000 que se pueden expresar de más maneras distintas como suma de dos primos?

Por ejemplo 26 se puede escribir de 5 maneras distintas porque 26 = 3+23 = 7+19 = 13+13 = 19+7 = 23+3 .

(Nota: 0 y 1 no son primos)

3

¿Cuántos pares de números enteros (a, b) existen tales que 0<a<b<1000 y además a + (a+1) + ... + (b-1) + b es múltiplo de 30?

Nivel 3 (11^er año de escolaridad en adelante)

1

Un número n es entretenido si cumple simultáneamente con las siguientes dos condiciones:

i) De los dígitos de n, el mas grande aparece exactamente una vez.

ii) Si a n se le quita su dígito más grande queda un número primo.

Hallar la cantidad de números entretenidos menores que 1000000.

(Nota: 0 y 1 no son primos)

2

Para cada número entero A se define la siguiente sucesión:

s(1) = A

s(2) = 2000

si n>=1, s(n+2) es el resto de hacer (s(n))² dividido s(n+1).

La sucesión termina al obtener un resto 0.

a) Probar que, para cualquier A, la sucesión siempre termina.

b) La longitud de la sucesión es la posición del termino 0. Por ejemplo, si A = 9, las sucesión es 9, 2000, 81, 58, 7, 4, 1, 0 y su longitud es 8. ¿Cuál es la longitud máxima posible? Justificar.

3

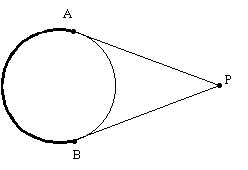
Se tiene una circunferencia de radio 1 y un punto P exterior. Se determinan dos puntos distintos A y B sobre la circunferencia de manera que las rectas PA y PB sean tangentes a la circunferencia. Determinar la distancia entre P y el centro de la circunferencia si la suma de las longitudes de los segmentos PA y PB es igual a la longitud del arco de circunferencia AB más alejado de P. Aproximar el resultado con por lo menos 3 decimales.

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar