Métodos de elección:
Siguiendo (Steen, 1994) resumiremos algunos métodos matemáticos de elección entre varios candidatos (o alternativas) C1, C2, ..., Cn.
Método de pluralidad. Cada votante dá un voto al candidato preferido y el que obtiene mayor cantidad de votos es declarado vencedor.
Método secuencial de mayorías. Cada votante dá su voto al candidato preferido y gana el que obtiene más de la mitad más uno de los votos. Si ello no se da, en una segunda ronda donde concurren los dós candidatos más votados se busca de nuevo quien alcance la mayoría.
Método secuencial eliminatorio. Cada votante da su voto al candidato preferido y en la primera ronda se elimina el menos votado, en la segunda el menos, etc., hasta llegar al candidato "ideal".
Método de Borda. Cada votante emite listas preferenciales de candidatos (ordenados) y a partir de dichas listas se dan a cada candidato tantos puntos (pesos) como candidatos quedan por debajo de el en las listas (o pesos según número ordinal en las listas) y así se suman ponderalmente los votos recibidos.
Método de Concorcet. Cada candidato es comparado con cualquier otro mirando con cuantos ha superado el otro en las listas de preferencias.
Considere la siguiente votación (Malkevich) emitida por 55 votantes sobre 5 candidatos C1, C2, C3, C4, C5:
| 1°
2° 3° 4° 5° |
C1 C4 C5 C3 C2 |
C2 C5 C4 C3 C1 |
C3 C2 C5 C4 C1 |
C4 C3 C5 C2 C1 |
C5 C2 C4 C3 C1 |
C5 C3 C4 C2 C1 |
| Votos: | 18 | 12 | 10 | 9 | 4 | 2 |
Aplique los cinco métodos para designar en cada caso el ganador. Compare ventajas e inconvenientes entre estos métodos.
Un método por escanios políticos por simple proporcionalidad
Si V1,
V2, ..., Vn son los votos obtenidos por
n partidos que deben ocupar e escaños
parlamentarios, calcúlese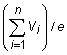 
para saber el número de votos por
escaño y a continuación asígnese a cada partido el número
de escaños que le toca redondeando por exceso los restos
mayores.
Aplique a esta distribución a repartir 6 escaños entre tres partidos que obtuvieron respectivamente 103.400 votos, 248.000 votos y 52.080 votos.
Un método de escaños políticos por sucesión de divisores
Sean V1 
V2 ... Vn los votos (ordenados) de n
partidos que deben repartirse e escaños. Fíjese
una sucesión 0 < d1 < d2 <
... < d e y divídase cada Vi por
los e números (Vi/d1, Vi/d2,
..., Vi/de). Forme así una matriz con
las n filas y e columnas de las divisiones y márqunse las e
cantidades mayores den esta matriz. Asígnense tantos
escaños a cada partido como números mayores aparecen en
cada fila correspondiente.
Son usuales las sucesiones:
Imperiali: 2, 3, 4, 5, 6, ...
D'Hondt: 1, 2, 3, 4, 5, ...
St-Lagüe I: 1, 3, 5, 7, 9, ...
St-Lagüe II: 1, 4, 3, 5, 7, 9, ...
Danés: 1, 4, 7, 10, 13, ...
Se tienen que repartir 9 escaños entre 5 partidos que han obtenido 700.000 votos, 500.000 votos, 400.000 votos, 200.000 votos, 30.000 votos. Proponga distintas situaciones usando diferentes sucesiones y compare resultados.
Método de votaciones ponderadas.
Considere una
situación con n votantes v1, v2, ...,
vn cada uno de los cuales puede emitir p(v1),
p(v2), ..., p(vN) votos sobre un asunto
y sea c la cuota de votos necesarios para aprobar el asunto.
Por ejemplo Vi puede ser un partido político, p(Vi)
los parlamentarios de dicho partido y c los votos necesarios
para elegir un presidente. Por ejemplo c puede ser el 51% de
los votos y v1, v2, v3 tres
accionistas que poseen el 49%, 48% y 3% de las acciones.
El índice de poder de Banzhaf de un votante
vi es el número de las distintas coaliciones que
ganarían al juntarse con vi más el número de
distintos bloques de coaliciones que ganarían con vi.
El índice de poder de Shapley-Shubik de un
votante vi es la relación entre el número de
permutaciones entre v1, v2, ..., vn
en donde la presencia de vi es decisiva y el
número total de permutaciones posibles. Se anotan junto a
cada posible permutación el peso del primer votante, el peso
de los dos primeros, etc. y se marca cuando aparece el
número que supera la nota q indicándose entonces el votante
que resulta esencial (pivot). El índice divide los casos
donde se es pivot por n!.
