V Certamen el Número de Oro. 1997
Soluciones a los problemas

(Esta página está pensada para consultarse on-line y posiblemente imprimirla con su browser. Bajarse la página es complicado por la cantidad de imágenes que tiene. Le aconsejo, en caso de querer conservar una copia, bajarse el archivo de word oro97sol.zip. El archivo está comprimido. Si no puede descomprimirlo, puede bajar el winzip para windows95 de http://www.oma.org.ar/ftp/winzip70.exe.)

webmaster@oma.org.ar

Profesores de enseñanza media

1

Determine todos los números primos de la forma .

La sucesión 2, 2², 2²², ... está definida de tal forma que cada término es el cuadrado del anterior. Sus primeros valores son 2, 4, 16, 256, etc., y podemos observar la repetición del 6 como último dígito. Puesto que 6² = 36 6 (10), resulta que todos los términos a partir del tercero terminarán en 6, de donde se concluye que al sumar 9 el número obtenido terminará en 5, no siendo en consecuencia un número primo (obviamente es mayor que 5). Los únicos números primos de la forma indicada son entonces los que corresponden a los dos primeros términos, a saber: 11 y 13

2

Un polinomio f de grado 2 con coeficientes reales es tal que toda permutación de sus coeficientes determina un polinomio con las mismas raíces que f . Calcule dichas raíces.

Sea f = aX² + bX + c. Observemos en primer término que 0 no es raíz de f, pues en tal caso también sería raíz del polinomio cX² + bX + a, de donde resultaría que a es nulo. Esto es una contradicción, pues f es de grado 2. Veamos también que f no puede tener una raíz doble. En efecto, si r es una raíz doble de f, tendríamos

f = a(X - r)² = aX² - 2arX + ar².

Permutando el término lineal y el constante, r debiera ser la única solución de la ecuación

0 = ar² + ar³ - 2ar = ar(r + r² - 2),

que, sin embargo, tiene dos soluciones distintas, 1 y -2 (obsérvese que r es distinto de cero).

En consecuencia, podemos suponer que f tiene dos raíces distintas. En particular, f tiene una raíz a1. Usando la hipótesis, resulta que valen las igualdades:

aa² + ba + c = 0
ba² + aa + c = 0
aa² + ca + b = 0

Restando la segunda de la primera se obtiene a(a - b)(a -1) = 0, de donde sigue que a = b, pues a es distinto de cero y de uno. Si ahora restamos la tercera de la primera, tenemos: (b - c)(a - 1) = 0, esto es, a=b=c. Por lo tanto, f = a(X² + X + 1), cuyas raíces son , como se verifica por simple aplicación de la conocida fórmula.

3

Las tres bisectrices de un triángulo son de longitud menor ó igual que uno. Demuestre que el área del triángulo es menor ó igual que .

Designemos por A, B y C a los vértices del triángulo, y supongamos que  es el menor de sus ángulos. Por lo tanto, Â/3, y en consecuencia cos  cos /3 = /2, ya que el coseno es decreciente entre 0 y p. Si AD es la bisectriz correspondiente al ángulo Â, consideremos las proyecciones ortogonales de los puntos B y C sobre la recta determinada por AD, que notaremos B' y C', respectivamente. Puesto que B, D y C están alineados, resulta que alguno de los dos segmentos AB' y AC' tiene longitud menor o igual que AD. Supongamos sin pérdida de generalidad que AB'AD.

En el triángulo rectángulo AB'B tenemos: cos Â=AB'/AB, de donde sigue que

.

Si calculamos ahora el área tomando como base el lado AB, y teniendo en cuenta que la altura h correspondiente al vértice C es menor o igual que la bisectriz del ángulo C, concluimos que

,

como queríamos probar.

 

4

En una reunión de 20 personas hay exactamente 49 pares de personas que se conocían entre sí. Pruebe que alguna persona conocía a lo sumo a 4 de los asistentes.

Designando a las personas por P₁, P₂, ..., P₂₀, construimos una matriz de 20x20 según las siguientes reglas: si ij, en la posición (i , j) escribimos un uno si P_i conoce a P_j, y un cero en caso contrario. En las posiciones (i , i) simplemente colocamos un asterico.

La hipótesis del problema asegura que en la matriz hay exactamente 49x2=98 unos, ya que si en la posición (i , j) hay un uno también lo habrá en la posición (j , i). Ahora bien, si en cada fila hubiera al menos 5 unos, el número total de unos sería al menos 100, ya que hay 20 filas. En consecuencia, en alguna fila hay a lo sumo 4 unos, esto es, alguna persona conocía a lo sumo 4 de los asistentes, como queríamos demostrar.

 

5

Demuestre que es posible elegir 17 segmentos de longitudes enteras menores ó iguales que 1997, de manera que con ninguna terna de ellos pueda construirse un triángulo. ¿Pueden elegirse también 18 segmentos con las mismas características?

Veamos en primer término que no pueden elegirse 18 segmentos de longitudes enteras menores o iguales que 1997 de manera que tres cualesquiera de ellos no determinen un triángulo, lo que nos dará la pista para resolver la primera parte del problema. Recordemos que dadas tres cantidades positivas abc, la condición necesaria y suficiente para que exista un triángulo con dichas cantidades como longitudes de sus lados es que c < a + b.

Supongamos que podemos elegir 18 segmentos de longitudes enteras m₁m₂...m₁₈1997 de manera que cualquier terna de ellos no determine un triángulo. Tenemos entonces las desigualdades:

m₁1 ; m₂1 ; m₃m₁+m₂ 2 ; m₄ m₂ + m₃ 3 ; m₅ m₃ + m₄ 5 .....,

y así siguiendo. Si observamos la ley de formación del miembro de la derecha de las desigualdades precedentes, observamos que cada uno es la suma de los dos anteriores, la misma que la regla de formación de los términos F_k de la sucesión de Fibonacci. Más aún, los dos primeros términos (ambos igual a 1), coinciden con los dos primeros números de Fibonacci F₁ y F₂. Deducimos entonces que m_iF_i para todo i. En particular, resulta que m₁₈F₁₈ = 2584, lo que es una contradicción.

Lo anterior nos permite resolver la primera parte del problema. En efecto, tomemos 17 segmentos de longitudes F₁, F₂, F₃, ..., F₁₇. Dada cualquier terna de ellos, digamos F_i, F_j y F_k, con los índices dados en forma creciente, tenemos: F_k = F_k-1+F_k-2F_j+F_i, y por lo tanto no determinan un triángulo. Además, estas cantidades satisfacen los requerimientos del problema, ya que F_sF₁₇ = 1597 < 1997, para todo índice s.

 

6

Sea . ¿Cuál de los dos números es más grande: ln²(n) ó ln(n-1).ln(n+1)?

Siendo n3, las dos cantidades ln(n-1) y ln(n+1) son positivas. Aplicándoles la fórmula que establece que la media geomética entre dos números positivos y distintos es menor que su media aritmética, obtenemos:

.

Elevando al cuadrado concluimos que

ln(n-1).ln(n+1) < ln²(n).

7

¿Existen cuatro números naturales consecutivos cuyo producto sea un cuadrado perfecto?

Daremos respuesta negativa al problema mostrando que el producto de cuatro números naturales consecutivos es siempre de la forma a²-1, que sólo es un cuadrado si a=1, caso que claramente queda excluido. Para ello, designemos por n, n+1, n+2 y n+3 a tales números. Completando sucesivamente cuadrados, tenemos:

como queríamos probar.

 

8

Sea P un punto interior de un hexágono regular. Se une P con cada vértice del hexágono, determinando así 6 triángulos, que coloreamos alternativamente de rojo y azul. Pruebe que la suma de las áreas de los 3 triángulos rojos coincide con la suma de las áreas de los 3 triángulos azules.

Sean V₁, V₂, ..., V₆ los vértices del hexágono, y supongamos que los triángulos coloreados de azul son V₁PV₆ , V₂PV₃ , V₄PV₅. Consideremos ahora el triángulo ABC que se obtiene al prolongar los lados exteriores de los triángulos azules, como se indica en la figura. Puesto que los ángulos interiores de un hexágono regular miden 120°, sigue inmediatamente que ^A = ^B = ^C = 60°, esto es, ABC es un triángulo equilátero. Más aún, si L es la longitud de sus lados y la de los lados del hexágono, es fácil ver que se verifica la relación L=3.

Calculemos ahora la suma S de las áreas de los triángulos azules. Tenemos:

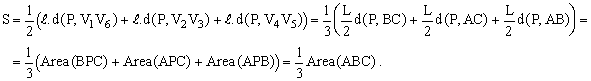
Si realizamos una construcción análoga para los triángulos rojos, queda determinado un triángulo A'B'C' que, por razones evidentes de simetría, resulta igual al ABC. Si S' es la correspondiente suma de áreas, concluimos entonces que S = S', como queríamos probar.

 

9

Tres deportistas disputarán entre sí una serie de pruebas atléticas, hasta que alguno de los participantes obtenga 3 triunfos. Se dará entonces por finalizada la competencia y se lo declarará ganador. ¿Cuál es el número más probable de pruebas a realizarse?

Es claro que deberán realizarse por lo menos 3 pruebas y a lo sumo 7, ya que en este último caso es imposible que cada competidor gane a lo sumo dos pruebas, hecho que sí puede ocurrir transcurridas 6 pruebas (2 pruebas cada uno). Habrá que calcular entonces la probabilidad de que la competencia se decida en m pruebas para cada valor de m entre 3 y 7.

El caso m=3 es el más sencillo de todos. La única posibilidad es que alguno de los participantes gane sucesivamente las tres. Puesto que la probabilidad de ganar cada prueba es 1/3 y el atleta que puede ganar es cualquiera de los tres, resulta que la probabilidad de que la competencia se decida en el tercer evento es 3.(1/3)³ = 1/9. En los restantes casos el análisis es algo más complicado. A manera de ejemplo, resolveremos con detalle el caso m=5.

Se presentan dos subcasos, a saber:

1. Un participante (A) gana tres pruebas y otro (B) gana las dos restantes. El número de situaciones posibles para la eleccion de ambos atletas es entonces 6, ya que hay 3 formas de elegir A y dos de elegir B. Debemos ahora analizar las posibles secuencias en que se obtienen los triunfos. Es claro que la última prueba debe ganarla A. En cuanto a las cuatro primeras, dos gana A y otras dos B, en cualquier orden. Deberemos considerar entonces las permutaciones con repetición de los 4 símbolos AABB, cuyo número total es . Tenemos entonces 6x6 = 36 posibles formas.
   
   
2. Un participante (A) gana tres pruebas y los dos restantes (B y C) una cada una. Aquí la elección de los atletas se puede hacer de 3 maneras, pues sólo hay que elegir A. En cuanto a las posibles secuencias, nuevamente la última prueba debe ganarla A, y para las cuatro primeras debemos considerar todas las ordenaciones de los símbolos AABC, cuyo número total es . Tenemos entonces 3x12 = 36 posibles formas también en este subcaso.

Luego hay 36+36 = 72 formas de que la competencia se decida en 5 pruebas, ya que i. y ii. son mutuamente excluyentes. En consecuencia (teniendo en cuenta que cada prueba es independiente de la anterior), la probabilidad de este suceso es 72x(1/3)⁵=8/27 .

Argumentando en forma similar, resulta que los respectivos valores de la probabilidad para los sucesivos valores de m son 1/9, 2/9, 8/27, 20/81 y 10/81, siendo 8/27 el mayor de ellos (Ud. puede verificar que la suma de los mismos es 1, como corresponde). En definitiva, el número de pruebas más probable a realizarse es 5.

 

10

Si c es un número real positivo, consideremos la sucesión

Pruebe que converge al número de oro .

Designando por x_n al n-ésimo término de la sucesión, vemos que la misma está definida por la recurrencia:

.

Probaremos que la sucesión es monótona. Observemos previamente que es la única raíz positiva del polinomio f = X² - X - 1, verificándose entonces las desigualdades:

Distinguiremos ahora dos casos:

1. . Afirmamos que en tal caso la sucesión es creciente y todos sus términos son menores que . En efecto, x₁< por hipótesis. Suponiendo por hipótesis inductiva x_n<, tenemos que (x_n)²-(x_n+1)²=(x_n)²-x_n-1<0, esto es, x_n<x_n+1. Además, (x_n+1)² = 1+x_n < 1+ = ², de donde x_n+1<. Luego, la sucesión es creciente y está acotada superiormente, y por lo tanto es convergente.
   
   
2. . En este caso, que se resuelve en forma muy similar al anterior, resulta que la sucesión es decreciente y todos sus términos son mayores ó iguales que el número de oro.

En cualquiera de ambas situaciones tenemos entonces que {x_n}converge, digamos a un número , obviamente positivo. Tomando ahora límite en la expresión (x_n+1)² = x_n+1, obtenemos que ² = +1. Luego, =, como queríamos probar.

IV Certamen el Número de Oro. 1997
Alumnos del Profesorado

1

¿Para qué valores de n el desarrollo decimal de 11ⁿ tiene sus últimas dos cifras iguales?

¿Y sus últimas tres cifras iguales?

Notemos que 11ⁿ 1ⁿ1 (10), esto es, cualquier potencia de 11 termina en 1. Por lo tanto, nos interesan aquellas potencias que terminan en 11, o sea, debemos caracterizar los números naturales n que satisfacen la congruencia 11ⁿ11 (100). Empleando la fórmula del binomio de Newton, tenemos:

,

pues a partir de k=2 todos los términos son múltiplos de 100. Luego,

11ⁿ11 (100) sii 10n 10 (100) sii n 1 (10).

Hemos probado entonces que 11ⁿ tiene sus últimas dos cifras iguales si, y sólo si, n termina en 1.

Supongamos ahora que 11ⁿ tiene sus últimas tres cifras iguales. Por lo anterior, n será de la forma 10s+1 y debe verificarse la congruencia 11ⁿ111 (10³). Empleando nuevamente la fórmula del binomio, tenemos: . Luego:

lo que claramente es imposible, por razones de paridad. En consecuencia, una potencia de 11 no puede terminar en tres cifras iguales.

2

Sean dados dos triángulos semejantes no iguales, y tales que dos lados de uno de ellos son respectivamente iguales a dos lados del otro. Determine los posibles valores de la razón de semejanza. Demuestre que cada valor obtenido es razón de semejanza de un par de triángulos satisfaciendo las condiciones del problema.

Designemos por abc las longitudes de los lados de un triángulo y por a'b'c' las del otro. Si >1 es la razón de semejanza, asumiremos que a' = a , b' = b y c' = c. Puesto que claramente a es menor que todos los lados del segundo triángulo, deducimos que debe ser a' = b y b' = c. Luego:

Teniendo en cuenta las relaciones que deben verificar los lados de un triángulo, tenemos , de donde sigue que ²--1 < 0. Puesto que el número de oro es la única raíz positiva del polinomio X² - X - 1, concluimos que 1 < < , lo que da una primera respuesta al problema.

Para completarla, debemos ver que dado cualquier en este rango, existen dos triángulos en las condiciones del problema. Para ello, consideremos las longitudes 1/ < 1 < . Las mismas determinan un triángulo, pues 1/ +1 = (1+)/ > ²/ = . Tomemos ahora un triángulo de longitudes 1, y ². Por razones idénticas a las anteriores, dicho triángulo está bien definido y es claro que ambos triángulos satisfacen las hipótesis del problema, con como razón de semejanza.

3

Pruebe que el polinomio x³ - 2x² + ax- 1/3 no puede tener todas sus raíces reales y positivas, cualquiera sea el número real a.

Supongamos que el polinomio dado admita tres raíces reales y positivas r, s y t. A partir de las relaciones entre las raíces y los coeficientes de un polinomio, resulta que la suma de las mismas es 2 y su producto es 1/3. Puesto que la media geométrica de tres números positivos no supera a su media aritmética, obtenemos: , ó, equivalentemente, . Elevando al cubo, resulta que 327/8, lo que claramente es una contradicción.

 

4

Supongamos que en la esfera de un reloj se altera arbitrariamente el orden usual de los números. Demuestre que cualquiera sea la permutación obtenida, siempre habrá una terna de números ocupando posiciones consecutivas de manera que la suma de los mismos sea mayor ó igual que 20.

Si a₁, a₂, ..., a₁₂ es la permutación de los números 1, 2, ..., 12 obtenida, consideremos las doce sumas S_i de ternas de números ocupando posiciones consecutivas, esto es,

.

Es claro que cada número entre 1 y 12 aparece como sumando en exactamente tres de estas sumas (por ejemplo, a₂ aparece en S₁, S₂ y S₁₂). Por lo tanto, si sumamos todos los S_i, obtenemos:

.

Dividiendo 234 por 12, vemos que el cociente es 19 y el resto es 6. Luego (Principio de los Casilleros), algún sumando S_k debe valer por lo menos 20, como queríamos probar.

 

5

Pruebe que es impar y compuesto.

 

Aplicando el Teorema de Fermat, resulta que (3¹¹)² = 3²² 1 (23). Siendo 23 un número primo, sigue que 3¹¹1 (23) ó 3¹¹-1 (23). Por otro lado, 37² (23) entonces 37² (23) entonces 3¹¹(7²)¹¹ = 7²²1 (23). Luego, 3⁷⁷ = (3¹¹)⁷1 (23). Esto significa que 23 divide a 3⁷⁷-1, y puesto que este es impar, también divide al número entero , que resulta así compuesto (obviamente es mayor que 23).
Si tomamos ahora congruencia módulo 4, tenemos: 3⁷⁷-1(-1)⁷⁷-1 = -22 (4). Es decir, el numerador es par y no divisible por 4. En consecuencia, es impar.

 

6

Dos alumnos colocan alternativamente números enteros en los lugares vacíos de la "ecuación"

x³ + ()x² + ()x + () = 0.

¿Dispone el alumno que realiza el primer movimiento de alguna estrategia que le permita asegurar que al finalizar el juego siempre se obtendrá una ecuación con tres soluciones enteras?

Veremos que el alumno que comienza el juego dispone de una estrategia ganadora. En el primer movimiento, coloca un cero en el lugar vacío correspondiente al término de grado cero. Con esto se asegura que 0 será una solución, y el segundo alumno deberá continuar con la "ecuación" X³ + ()X² + ()X = 0. Supongamos que coloque un entero a en cualquiera de los dos lugares libres disponibles. Entonces el primero coloca el entero -(a+1) en el otro. En cualquier caso, la suma de los coeficientes ubicados es cero, por lo que 1 es solución de la ecuación. Además, se verifica inmediatamente que la tercera solución también es entera, siendo a ó -(a+1) según los casos. En definitiva, el primer alumno gana el juego.

 

7

Dado un triángulo, determine en su interior un punto O tal que el producto OP.OQ.OR sea máximo, siendo P, Q y R los pies de las perpendiculares a los lados que pasan por O.

Designemos por A, B y C los vértices del triángulo y por a, b y c las longitudes de los correspondientes lados opuestos. Si O es un punto interior, puesto que el área del triángulo ABC es la suma de las áreas de los triángulos OBC, OAC y OAB, obtenemos la fórmula 2 = a.OP + b.OQ + c.OR. Deberemos entonces maximizar el producto xyz, donde x, y, z es una terna de números positivos sujetos a la relación ax+by+cz = 2(*).

Para ello, consideremos la terna , que claramente satisface la relación. Veamos, usando la desigualdad entre la media geométrica y la aritmética, que su producto es máximo. En efecto, si x, y, z, verifica (*), tenemos:

.

Consideremos ahora el punto interior G de ABC determinado por la intersección de sus medianas, esto es, el baricentro del triángulo. Es bien conocido que en ese caso los triángulos GBC, GAC y GAB tienen igual área, siendo entonces /3 el área común de los tres. Tomando por ejemplo el triángulo GBC tenemos: . Análogamente, resulta que GQ = y₀ y GR = z₀. Por lo que hemos demostrado, el producto GP.GQ.GR es entonces máximo.

8

Sea f una función de R en R, con dos derivadas continuas, verificando las condiciones:

Demuestre que existe tal que .

Sea M el máximo de la función |f ''(x)| en el intervalo [0,1]. Aplicando a f '(x) el teorema del valor medio, sigue que . En particular, tomando sucesivamente x=0 y x=1, y usando las hipótesis del problema, obtenemos las desigualdades

para todo y en el intervalo [0,1] .

Además, . Tomando ahora valor absoluto, tenemos:

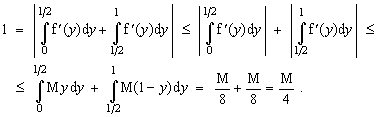
Luego, M 4, como queríamos probar.

9

Tres deportistas disputarán entre sí una serie de pruebas atléticas, hasta que alguno de los participantes obtenga 3 triunfos. Se dará entonces por finalizada la competencia y se lo declarará ganador. ¿Cuál es el número más probable de pruebas a realizarse?

Es claro que deberán realizarse por lo menos 3 pruebas y a lo sumo 7, ya que en este último caso es imposible que cada competidor gane a lo sumo dos pruebas, hecho que sí puede ocurrir transcurridas 6 pruebas (2 pruebas cada uno). Habrá que calcular entonces la probabilidad de que la competencia se decida en m pruebas para cada valor de m entre 3 y 7.

El caso m=3 es el más sencillo de todos. La única posibilidad es que alguno de los participantes gane sucesivamente las tres. Puesto que la probabilidad de ganar cada prueba es 1/3 y el atleta que puede ganar es cualquiera de los tres, resulta que la probabilidad de que la competencia se decida en el tercer evento es 3.(1/3)³ = 1/9. En los restantes casos el análisis es algo más complicado. A manera de ejemplo, resolveremos con detalle el caso m=5.

Se presentan dos subcasos, a saber:

1. Un participante (A) gana tres pruebas y otro (B) gana las dos restantes. El número de situaciones posibles para la eleccion de ambos atletas es entonces 6, ya que hay 3 formas de elegir A y dos de elegir B. Debemos ahora analizar las posibles secuencias en que se obtienen los triunfos. Es claro que la última prueba debe ganarla A. En cuanto a las cuatro primeras, dos gana A y otras dos B, en cualquier orden. Deberemos considerar entonces las permutaciones con repetición de los 4 símbolos AABB, cuyo número total es . Tenemos entonces 6x6 = 36 posibles formas.
   
   
2. Un participante (A) gana tres pruebas y los dos restantes (B y C) una cada una. Aquí la elección de los atletas se puede hacer de 3 maneras, pues sólo hay que elegir A. En cuanto a las posibles secuencias, nuevamente la última prueba debe ganarla A, y para las cuatro primeras debemos considerar todas las ordenaciones de los símbolos AABC, cuyo número total es . Tenemos entonces 3x12 = 36 posibles formas también en este subcaso.

Luego hay 36+36 = 72 formas de que la competencia se decida en 5 pruebas, ya que i. y ii. son mutuamente excluyentes. En consecuencia (teniendo en cuenta que cada prueba es independiente de la anterior), la probabilidad de este suceso es 72x(1/3)⁵=8/27 .

Argumentando en forma similar, resulta que los respectivos valores de la probabilidad para los sucesivos valores de m son 1/9, 2/9, 8/27, 20/81 y 10/81, siendo 8/27 el mayor de ellos (Ud. puede verificar que la suma de los mismos es 1, como corresponde). En definitiva, el número de pruebas más probable a realizarse es 5.

 

10

Si c es un número real positivo, consideremos la sucesión

Pruebe que converge al número de oro .

Designando por x_n al n-ésimo término de la sucesión, vemos que la misma está definida por la recurrencia:

.

Probaremos que la sucesión es monótona. Observemos previamente que es la única raíz positiva del polinomio f = X² - X - 1, verificándose entonces las desigualdades:

Distinguiremos ahora dos casos:

1. . Afirmamos que en tal caso la sucesión es creciente y todos sus términos son menores que . En efecto, x₁< por hipótesis. Suponiendo por hipótesis inductiva x_n<, tenemos que (x_n)²-(x_n+1)²=(x_n)²-x_n-1<0, esto es, x_n<x_n+1. Además, (x_n+1)² = 1+x_n < 1+ = ², de donde x_n+1<. Luego, la sucesión es creciente y está acotada superiormente, y por lo tanto es convergente.
   
   
2. . En este caso, que se resuelve en forma muy similar al anterior, resulta que la sucesión es decreciente y todos sus términos son mayores ó iguales que el número de oro.

En cualquiera de ambas situaciones tenemos entonces que {x_n}converge, digamos a un número , obviamente positivo. Tomando ahora límite en la expresión (x_n+1)² = x_n+1, obtenemos que ² = +1. Luego, =, como queríamos probar.

Archivo de Enunciados Oro Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar