- VII-223 (Segundo nivel)
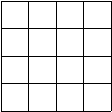
En la cuadrícula de la figura se quieren pintar de rojo 4 cuadraditos de modo que un cuadradito rojo no tenga a su alrededor ningún otro rojo.
¿De cuántas maneras distintas se puede hacer?
Problemas Semanales
| 28 de Agosto de 1998 |
| OMA |
Decidir si es posible que un conjunto de cinco números naturales distintos tenga la siguiente propiedad:
Para cada par de números del conjunto, al multiplicar los dos números se obtiene un múltiplo de la suma de los dos números.
Diremos que un número natural es travieso si su desarrollo binario tiene una cantidad impar de dígitos 1. Por ejemplo, 4 es travieso porque su desarrollo binario es 100, que tiene una cantidad impar de dígitos 1; 6 no es travieso, porque su desarrollo binario es 110, que tiene una cantidad par de dígitos 1.
Determinar la cantidad de números traviesos que son menores o iguales que 1997.
Los cuatro lados de un trapecio isósceles son tangentes a una circunferencia y los puntos de tangencia son vértices de un cuadrilátero cuya área es 4/9 del área del trapecio.
Si a es la base menor del trapecio y b es la base mayor del trapecio, hallar a/b.
| 28 de Agosto de 1998 |
| ÑANDÚ |
Por $ 7 se compran: 5 alfajores, 1 chocolate y 4 turrones.
Cada alfajor cuesta un tercio de lo que cuesta un chocolate.
Cada chocolate cuesta el doble de lo que cuesta un turrón.
¿Cuál es el precio de cada golosina?
|
|
Dos trenes parten de la estación Las Golondrinas en la misma dirección.
El primero sale a las 12 hs y avanza a 60 km/h, el segundo sale por una vía rápida, a las 15 hs y marcha a 100 km/h.
¿A qué hora y a qué distancia de Las Golondrinas el tren más veloz pasa al primero?
 Problemas
Semanales Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |