OMA - Problemas semanales. 22-5-98

Problemas Semanales

22 de Mayo de 1998

OMA

XV-111. (Primer Nivel)

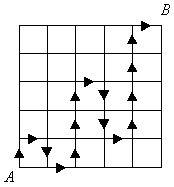
¿De cuántas maneras puede unirse A con B moviéndose sobre la cuadrícula si no está permitido pasar dos veces por el mismo lugar ni moverse hacia la izquierda? La figura muestra un camino posible.

XV-211. (Segundo Nivel)

Se marcaron en una recta 1997 puntos y se pintaron de azul o rojo. A continuación se colorearon los segmentos entre puntos consecutivos:

Si los dos extremos eran rojos, el segmento se pintó de rojo.

Si los dos extremos eran azules, el segmento se pintó de azul.

Si los dos extremos eran de distinto color, el segmento se pintó de blanco.

Al finalizar, hay 100 segmentos blancos y se sabe además que el primer punto era rojo. Decidir si con esta información es posible determinar con seguridad el color del último punto.

XV-311. (Tercer Nivel)

Hallar las tres últimas cifras de la derecha del número 19⁹⁷.

22 de Mayo de 1998

ÑANDÚ

VII-111 (Primer nivel)

Colocar en cada casillero uno de los siguientes números: 1 - 2 - 3 - 1 - 2 - 3 - 1 - 2 - 3 de modo que, la suma de los números de cada fila (horizontal), la suma de los números de cada columna (vertical) y la suma de los números de cada diagonal sea la misma.

VII-211 (Segundo nivel)

Se quieren escribir los números del 1 al 16, uno en cada casillero y sin repetir, de modo que la suma de los números de cada fila sea 34 y la suma de los números de cada columna sea 34.
Algunos números ya están ubicados, ¿cómo se pueden ubicar los restantes?

VII-311 (Tercer nivel)

ABDE es un rectángulo, BD = 2AB ,
ABCF es un cuadrado,
los arcos AF y BC son semicircunferencias.
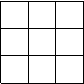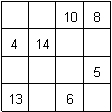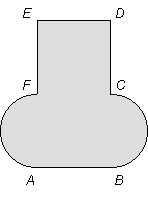La figura rayada tiene 142,8 cm de perímetro.
¿Cuál es el área de la figura sombreada?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina www.oma.org.ar \| info@oma.org.ar
mensajes webmaster@oma.org.ar