- VII-306 (Tercer nivel)
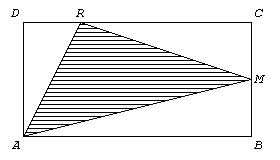
El rectángulo ABCD tiene 32cm2 de área.
M es punto medio de BC.
AB = 2.AD
DR = BM
¿Cuál es el área del triángulo ARM?
Problemas Semanales
| 17 de Abril de 1998 |
| OMA |
Una hoja de papel rectangular se divide mediante un sólo corte en un triángulo y un pentágono. Las longitudes de los lados del pentágono son 17, 25, 28, 33 y 43, en algún orden. Calcular el área del pentágono.
Sea ABC un triángulo obtusángulo con ^A < ^C < ^B.La bisectriz exterior del ángulo ^A intersecta a la prolongación del lado CB en X y la bisectriz exterior del ángulo ^B intersecta a la prolongación del lado AC en Y. Si AX = AB = BY, calcular la medida del ángulo ^A.
NOTA:
- En un triángulo ABC, la bisectriz exterior del ángulo ^A es la recta perpendicular a la bisectriz de ^A que pasa por A.
- ^A es "el ángulo A"
Sean A, B, C, D puntos de una circunferencia tales que AB es perpendicular a CD y sea P el punto de intersección de AB y CD. Si AP = 8, DP = 6, CP = 15, calcular el diámetro de la circunferencia.
| 17 de Abril de 1998 |
| ÑANDÚ |
En un torneo de tenis participan 16 jugadores.
En cada ronda cada jugador juega un partido, si gana pasa a la ronda siguiente, si pierde queda eliminado.
¿Cuántos partidos deben jugar en total para que quede definido el ganador del torneo?
Con los dígitos: 1 - 2 - 3 - 4 - 5 y 0 ,
¿cuántos números de cuatro cifras que son múltiplos de 5 y tienen todas las cifras distintas se pueden armar?
Explica por qué.
|
|
 Problemas
Semanales Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |