OMA - Problemas semanales. 16-10-98

Problemas Semanales

16 de Octubre de 1998

OMA

XV-130. (Primer Nivel)

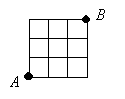
Un cuadrado de 3x3 se ha dividido en cuadraditos de lado 1 (ver figura). Una hormiga sale del punto A, camina por las líneas de la cuadrícula y llega a B. Los únicos puntos por los que puede pasar más de una vez son los vértices de los cuadraditos. ¿Cuál es la máxima longitud que puede tener el camino de la hormiga?

XV-230. (Segundo Nivel)

Sea n un número natural con cuatro o más divisores naturales. De todos los divisores de n, se consideran los cuatro más pequeños: a < b < c < d.

Hallar todos los n tales que

n = a² + b² + c² + d².

ACLARACIÓN: Notar que cualquiera sea n, el divisor más pequeño es 1.

XV-330. (Tercer Nivel)

Dados en el plano dos segmentos no paralelos AB y CD, hallar el lugar geométrico de los puntos P del plano tales que el área del triángulo ABP es igual al área del triángulo CDP.

16 de Octubre de 1998

ÑANDÚ

VII-130 (Primer nivel)

ABCD rectángulo, 5 AB = 6 BC
M es un punto de CD tal que MC = BC
N es el punto medio de MB
¿Qué fracción del rectángulo ABCD representa el cuadrilátero AMCN?

VII-230 (Segundo nivel)

A es el punto de la figura.
Se dibujan 7 segmentos con un extremo en A.
Se eligen algunos extremos libres de los segmentos dibujados (distintos de A; A no es un extremo libre) y se dibujan 7 segmentos con un extremo en cada uno de los puntos elegidos.
(ver ejemplo en la figura)
Se continúa este proceso.
¿Es posible, después de varios pasos, tener:

55 extremos libres?

1997 extremos libres?

Explica por qué.

VII-330 (Tercer nivel)

La circunferencia de centro O tiene 5 cm de radio.
El triángulo ABC tiene 84 cm de perímetro y sus lados son tangentes a la circunferencia de centro O.
Los arcos de circunferencia con centro en cada vértice del triángulo tienen 4 cm de radio.
¿Cuál es el área de la zona rayada?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina www.oma.org.ar \| info@oma.org.ar
mensajes webmaster@oma.org.ar