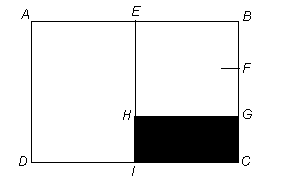Problemas Semanales
| 16 de Abril de 1999 |
| ÑANDÚ |
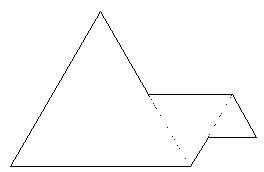
Con 3 triángulos equiláteros se armó esta figura.
El triángulo grande tiene 48 cm de perímetro.
El lado del triángulo mediano es la mitad del lado del triángulo grande. El lado del triángulo pequeño es la mitad del lado del triángulo mediano. ¿Cuál es el perímetro de la figura?
En el rectángulo ABCD:
E es el punto medio de AB, 2GC = EB, y G dividen a BC en 3 partes iguales.
El área de la zona sombreada es de 8 cm2.¿Cuál es el perímetro de la figura ABGHID?
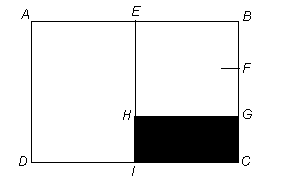
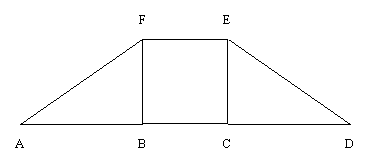
ADEF es un trapecio isósceles. BCEF es un cuadrado de 36 m2 de área.
Si el área del trapecio es el triple del área de BCEF, ¿cuánto mide AD?
| 16 de Abril de 1999 |
| OMA |
De los 999 números:
mcd(1;1998), mcd(2;1998), mcd(3;1998), ..., mcd(998;1998), mcd(999;1998),
¿cuántos son mayores que 19?
Aclaración: mcd denota máximo común divisor. Por ejemplo, mcd(6;9) = 3, mcd(54;36) = 18.
Dividir al conjunto
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
en dos grupos de ocho números cada uno de modo tal que en los dos grupos la suma de los ocho números sea la misma y en los dos grupos la suma de los cuadrados de los ocho números sea la misma.
En cada casilla de un tablero cuadriculado de 9 ´ 8 hay escrito un número real de modo tal que los números de cada fila forman una progresión aritmética y los números de cada columna forman una progresión aritmética. La suma de los números de las cuatro casillas de las esquinas es 98. Hallar la suma de todos los números del tablero.
 Problemas
Semanales Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |
