Problemas Semanales
| 12 de Junio 1998 |
| OMA |
Sean A y B dos números naturales de tres cifras cada uno. Si se escriben las cifras de A a continuación de las cifras de B se obtiene un número de seis cifras que es igual a 6 veces el número de seis cifras que se obtiene al escribir las cifras de B a continuación de las cifras de A. Hallar A y B.
Ariel, Bernardo y Claudio resuelven cada uno exactamente 60 problemas de una lista de 100. Todos los problemas fueron resueltos por al menos uno de los tres.
Diremos que un problema es fácil si los tres lo resolvieron y que es difícil si sólo uno de los tres lo resolvió.
Si d es la cantidad de problemas difíciles y f es la cantidad de problemas fáciles, hallar d - f.
Sean C y C' circunferencias tangentes interiores, de centros O y O', y radios R y r respectivamente (R>r).
La perpendicular por O' a la recta OO' intersecta a C en P y Q.
Sea M un punto de la recta OO' y en el interior de C tal que MP y MQ son tangentes a C'.
Sabiendo que ^PMQ = 90°, calcular R/r.
| 12 de Junio de 1998 |
| ÑANDÚ |
Todos los números enteros desde 0
hasta 2.000 se representan en un esquema donde los
números están unidos por flechas como muestra la
figura:
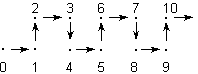
¿Podrías
representar la parte del esquema que corresponde a los
números desde 1992 hasta 1998?
Fer, Seba y Tomi ahorraron, entre los tres, $ 315.
Fer ahorró el 30% de lo que ahorró Seba.
Seba ahorró el 20% de lo que ahorró Tomi.
¿Cuánto ahorró cada uno ?
Matías tiene una cierta cantidad de ladrillos cúbicos todos iguales.
Cuando quiere construir una pared cuadrada, le faltan o le sobran ladrillos.
Lo mismo le ocurre si quiere armar un cubo.
Nicolás tiene el doble de ladrillos que Matías y puede construir una pared cuadrada usando todos los ladrillos.
Gabriela tiene el triple de ladrillos que Matías y puede armar un cubo usando todos los ladrillos.
¿Cuál es el menor número de ladrillos que puede tener Matías?
 Problemas
Semanales Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |