Problemas Semanales

• otras entregas
• suscribite a la lista de e-mail de problemas semanales

• XV-125. (Primer Nivel)

Sobre la mesa hay un papel cuadrado de 8 cm de lado al que se le ha recortado en una esquina un cuadrado de 1 cm de lado. Mariana debe dividir el papel en triángulos todos de igual área. ¿Cuál es el número mínimo de triángulos que tendrá esta división?

 

• XV-225. (Segundo Nivel)

El triángulo ABC tiene AB = 14, BC = 24 y AC = 15. Sean M en el lado AB y N en el lado BC tales que la recta MN divide al triángulo en dos figuras de igual área y de igual perímetro. Hallar la longitud de AM.

 

• XV-325. (Tercer Nivel)

Sea ABC un triángulo isósceles de base AB. Con centro en el punto medio de AB se traza la semicircunferencia tangente a los lados AC y BC del triángulo. Sean P en el lado AC y Q en el lado BC tales que PQ es tangente a la semicircunferencia. Si PA = a y QB = b, hallar la medida de AB en términos de a y b.

 

• VII-125 (Primer nivel)

Susana quiere ir a Mar del Plata. El pasaje en tren sale $ 30.
Por 8 días, el hotel que eligió cobra $ 448.
¿Cuánto gastará en total si decide quedarse sólo 5 días y la tarifa del hotel es proporcional a los días de estadía?

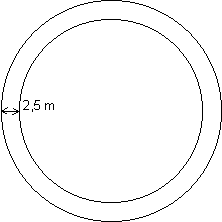
VII-225 (Segundo nivel) A lo largo de la circunferencia grande se plantaron 157 rosales, dejando 70 cm entre cada dos. La circunferencia interior es concéntrica con la grande y distante 2,5 m de ella. Si se quieren plantar también, 157 rosales equidistantes sobre la circunferencia menor ¿qué distancia habrá que dejar entre cada dos? Si se cubre con pasto el espacio entre las dos circunferencias ¿cuántos m quedan cubiertos de pasto?

• VII-325 (Tercer nivel)

Mezclando jugos de naranja, kiwi y pomelo se preparan los jugos A, B y C que se envasan en botellones de 5 litros.
Para 5 litros del jugo A se necesitan: 1 litro de jugo de naranja, 2 de jugo de kiwi y 2 de jugo de pomelo.
Para 5 litros del B se necesitan: 2 litros de jugo de naranja, 1 de jugo de kiwi y 2 de jugo de pomelo.
Para 5 litros del C se necesitan: 2 litros de jugo de naranja, 2 de jugo de kiwi y 1 de jugo de pomelo.
Utilizando exactamente 80 litros de jugo de naranja, 55 litros de jugo de kiwi y 70 litros de jugo de pomelo, ¿cuántos botellones de 5 litros de cada clase de jugo se pueden preparar?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar