Problemas Semanales

• otras entregas
• suscribite a la lista de e-mail de problemas semanales

• XV-118. (Primer Nivel)

Hallar un número natural de 97 dígitos, todos distintos de cero, que sea múltiplo de la suma de sus 97 dígitos.

 

• XV-218. (Segundo Nivel)

Hallar todos los números reales x que verifican

[19x + 97] = 19 + 97x .

ACLARACIÓN: Los corchetes indican la parte entera del número que encierran, por ejemplo,
[3,27] = 3; [1,25] = 1; [-2,7] = -3; [5] = 5; etc.

 

• XV-318. (Tercer Nivel)

Sean s y t dos rectas paralelas. Se han marcado k puntos en la recta s y n puntos en la recta t (k³ n). Si se sabe que la cantidad total de triángulos que tienen sus tres vértices en puntos marcados es 220, hallar todos los posibles valores de k y n.

• VII-118 (Primer nivel)

Sobre una circunferencia se marcan los puntos A, B, C, D, E y F a igual distancia entre sí.
Se dibujan polígonos convexos que tienen sus vértices en algunos o todos los puntos marcados.
¿Cuántos polígonos distintos se pueden dibujar?
¿Cuántos de estos polígonos son regulares?
De todos los polígonos que se pueden dibujar, ¿Cuál es el de mayor perímetro?

• VII-218 (Segundo nivel)

Con 24 fichas cuadradas de 9cm² de área, usándolas todas, sin superponerlas y sin dejar huecos, se arman rectángulos.
¿Es posible armar un rectángulo de 66 cm de perímetro?
¿Y uno de 72 cm de perímetro?
Explica por qué.

• VII-318 (Tercer nivel)

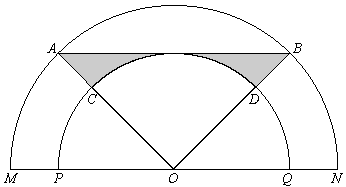
Los arcos MAN y PCQ son semicircunferencias de centro O.
El radio del menor es de 1 dm y el radio del mayor es de 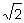dm.
^AOM = ^BON y ^AOB = 2 ^AOM (^ABC es el ángulo ABC)
¿Cuál es el área de la figura sombreada aproximada a cm²?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar