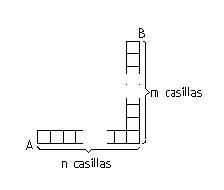Problemas Semanales

• otras entregas
• suscribite a la lista de e-mail de problemas semanales

• XV-109. (Primer Nivel)

Se considera un polígono regular de 10 lados. Hay que elegir tres vértices de este polígono de modo tal que el triángulo que determinan sea escaleno y ningún lado del triángulo sea al mismo tiempo lado del polígono de 10 lados. ¿De cuántas maneras distintas se pueden elegir los tres vértices?

 

• XV-209. (Segundo Nivel)

En cada casilla de un tablero cuadrado de 11x11 casillas se ha escrito un número mayor o igual que -1 y menor o igual que 1 (no necesariamente entero) de modo tal que la suma de los cuatro números ubicados en cada cuadrado de 2x2 sea siempre igual a 0. Hallar el máximo valor posible de la suma de los 121 números escritos en el tablero.

XV-309. (Tercer Nivel) Una hormiga camina por las líneas de un tablero de n + m - 1 casillas, como el de la figura, con n casillas de ancho y m casillas de alto (m2, n2). ¿De cuántas diferentes maneras puede ir desde A hasta B, si su camino no puede pasar dos veces por un mismo punto?

VII-109 (Primer nivel) En la figura se quiere pintar cada cuadradito de rojo o de azul. Los dos cuadraditos de la izquierda no pueden ser rojos a la vez. Los dos cuadraditos de la derecha no pueden ser rojos a la vez. ¿De cuántas maneras distintas puede hacerse?

• VII-209 (Segundo nivel)

  El cajero quería cobrar $315.
  El bibliotecario le dijo: -Esto es imposible, encuentre el error en su cuenta: llevo dos libros de cuentos de $16 cada uno, dos novelas de $18 cada una; cuatro diccionarios y dos manuales cuyos precios no recuerdo, lo que sí sé es que son valores enteros.
  ¿Cómo descubrió el bibliotecario el error?

VII-309 (Tercer nivel) En la figura: AC=BC y los ángulos miden lo que se indica: ACB = 30 ADE = 20 ¿Cuánto mide el ángulo CFD?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar