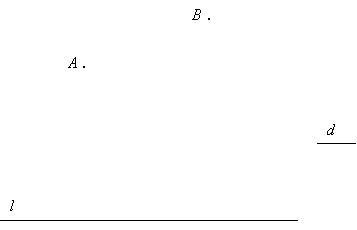
En la figura hay dos puntos, A y B, una recta l y un segmento de longitud d. Hallar dos puntos P y Q en la recta l de manera tal que el segmento PQ tenga longitud d y la suma AP+PQ+QB se la menor posible.
Problemas Semanales
| 2 de Octubre de 1998 |
| OMA |
En la figura hay dos puntos, A y B, una recta l y un segmento de longitud d. Hallar dos puntos P y Q en la recta l de manera tal que el segmento PQ tenga longitud d y la suma AP+PQ+QB se la menor posible.
Un geólogo tiene varias piedras y ninguna de ellas pesa más de 1 kg. Se sabe que si se separan las piedras en dos grupos, no importa de qué manera se haga, el peso total de uno de los dos grupos es menor o igual que 1 kg. Nada se sabe sobre la cantidad de piedras que tiene el geólogo ni se sabe cuánto pesa cada piedra. Hallar el valor máximo que puede tener el peso de todas las piedras juntas.
Sean ABC un triángulo y M el punto medio del lado AB. Si se sabe que ^CAM + ^MCB = 90°, demostrar que el triángulo ABC es isósceles o es rectángulo.
(^CAM es el ángulo CAM)
| 2 de Octubre de 1998 |
| ÑANDÚ |
La plaza de Ciudad Bella es un rectángulo de 100 m de ancho.
Se colocan alrededor de la plaza 320 árboles: uno en cada esquina y, sobre los lados, uno cada 2 m.
Si se quisiera marcar en la plaza una avenida central de 20 m de ancho y colocar los 320 árboles en los dos sectores que quedan: uno en cada esquina y los demás sobre los lados, de modo que la distancia cada dos árboles consecutivos sea siempre la misma, ¿qué distancia habría que dejar entre dos árboles consecutivos?
En una balanza de platillos,
- una botella y un vaso en el platillo izquierdo hacen equilibrio con una jarra en el platillo derecho.
- una botella sola equilibra un vaso y un plato y
- 3 de esos platos equilibran dos jarras iguales a la primera.
¿Cuántos vasos equilibran una botella?
En un tanque cilíndrico se echó agua hasta alcanzar 1,20 m de altura.
Sobre la base del tanque se apoyó un trozo cilíndrico de plomo que quedó totalmente sumergido y el nivel del agua dentro del tanque alcanzó 1,30 m.
¿Qué parte del volumen de agua se desplazó al colocar este trozo cilíndrico?
Si el trozo cilíndrico tiene 90 cm de altura, ¿cuál es la relación entre el radio del tanque y el radio de ese trozo de plomo?
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |