Problemas Semanales

• otras entregas
• suscribite a la lista de e-mail de problemas semanales

• XV-108. (Primer Nivel)

Matías ha dibujado un cuadrado ABCD con tinta negra y debe colorear con rojo todos los puntos P del interior del cuadrado tales que el área del cuadrilátero BCPA es igual al triple del área del cuadrilátero APCD. Describir cuál es la parte roja del dibujo y justificar.

 

• XV-208. (Segundo Nivel)

Si la mediana y la altura correspondientes a un mismo vértice de un triángulo dividen al ángulo en tres ángulos iguales, hallar los ángulos del triángulo.

 

• XV-308. (Tercer Nivel)

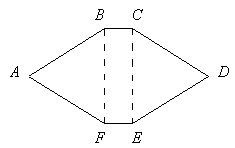
Sea ABCD un rectángulo inscrito en una circunferencia. Sea P un punto en el arco de la circunferencia. La paralela a AB que pasa por P intersecta a las prolongaciones de DA y CB en P₁ y P₂ respectivamente. La paralela a BC que pasa por P intersecta a AB y CD en P₃ y P₄ respectivamente. Demostrar que P₃ es el punto de intersección de las alturas del triángulo P₁P₂P₄.

VII-108 (Primer nivel) En la figura BF = 3 CB. El perímetro del rectángulo BCEF es de 24 cm. El perímetro del triángulo ABF es de 25 cm. Los triángulos ABF y CDE son isósceles e iguales. Hallar el perímetro del hexágono ABCDEF.

VII-208 (Segundo nivel) ACE es un triángulo equilátero. B, D y F son puntos medios de los lados del triángulo ACE. G, H e I son puntos medios de los lados del triángulo BDF. J, K y L son puntos medios de los lados del triángulo GFI. ¿Qué fracción del cuadrilátero ABDE representa la zona rayada?

• VII-308 (Tercer nivel)

Lucía fue a la feria del libro. Pagó $5 de entrada.
Compró varios libros y un diccionario. Los libros costaban $84; al agregar el diccionario, el total superaba los $100.
Por compras superiores a $100 se hace un descuento del 15% y, además, se devuelve el importe de la entrada.
Lucía pagó con un billete de $100 y uno de $20. Le devolvieron $14,50.
¿Cuál era el precio de venta del diccionario?

Problemas Semanales Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar