

Comentarios del Problema 3 - 12 / 10 / 2000
Esperamos sus mails en problematica@oma.org.ar
Sigamos con el tercer problema de Problemática 2000, que propusimos el 06/07/2000.
Lo recordamos:
| XVII-210 (Problemas semanales - OMA - Segundo nivel) |
| Sea ABC un triángulo isósceles, con AC = BC. La bisectriz de ángulo A intersecta al lado BC en D, y la bisectriz del ángulo C, intersecta al lado AB en E. Si AD = 2 CE, hallar la medida de los ángulos del triángulo ABC. |
Esta es la solución de Laura L.:
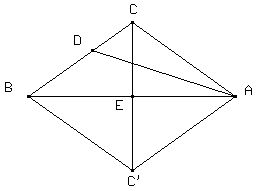
Tomamos C' como el
simétrico de C con respecto de AB. Entonces el DABC es igual al DABC', y CC' mide el doble
de CE, o sea que es igual a AD. Como DABC es isósceles, <CBA = <CAB = <C'AB
entonces, CB es paralela a AC', y el cuadrilátero CDC'A es un
trapecio. Como sus dos diagonales AD y CC' son iguales, resulta
que es un trapecio isósceles. Entonces, el <CC'A = <C'AD,
pero <CC'A = <C'CA, luego, <C'CA = <C'AD. Llamamos x
al ángulo <CAD. Como AD es bisectriz de <CAB, <DAB = x
, y
<BAC' = 2x. Por lo tanto, <DAC' = 3x = <C'CA. Pero
<C'CA = 90° - <CAB = 90° - 2x
3x = 90° - 2x
5x = 90°
x = 18° , <BAC = <ABC = 2x = 36° y <BCA = 180° - 36° - 36° = 108°
¿Soluciones, preguntas, dudas, problemas? Esperamos sus mails en problematica@oma.org.ar
| OmaNet - Educación Interactiva www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |