

Nota 3 - 31 / 03 / 2000
Esperamos sus mails en problematica@oma.org.ar
Nos escribió María Jose de Leon-Sotelo, pidiendo algunas pistas para los problemas de Pablo de la nota 1.
Recordemos estos problemas:
|
En el primer problema ella encontró una solución algebraica, pero en la nota 1 pedíamos encontrar una solución geométrica.
Una solución algebraica, quiere decir, que calculó la longitud de los lados del triángulo por ecuaciones. De todos modos, ese problema lo tomaron en un certamen de la OMA, y a los que hicieron una solución algebraica, se los dieron por bien.
Pero nos interesa ahora la solución geométrica. No vamos a dar la solución, esperamos que alguien nos la mande, pero veamos unas pistas:
Puedo pensar que tengo un segmento que mide 18 cm y uno que mide 5 cm.Tengo que descubrir cómo partir el segmento en tres, para formar los lados del triángulo.
Analicemos el problema al revés. Supongamos que yo ya tengo el triángulo construido:
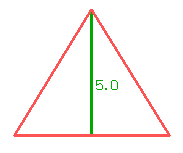
¿cómo hago para formar un segmento de 18cm?
Es simple: giro los lados hasta que queden todos alineados:
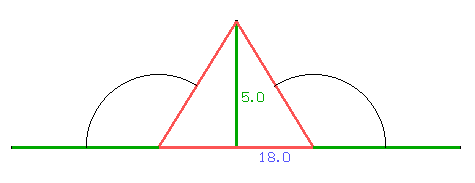
Esa figura que me quedó, ¡puedo construirla!
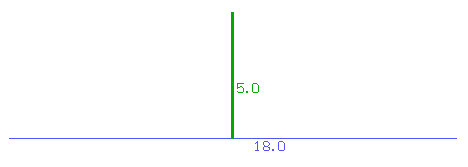
La pregunta entonces es: ¿cómo encuentro los dos puntos en donde tengo que partir el segmento de 18cm?
La respuesta es muy parecida a la solución del problema de la nota 1, justo antes del problema de Pablo.
Piensen, y después nos cuentan.
Vamos al problema 2:
Empecemos por algo más fácil:
Por ejemplo, hallar todos los n para los que (2n + 20) / (n + 5) es un entero.
Este problema es más parecido al problema original de la nota, sólo que hay un 2 multiplicando a n.
Pero es fácil, porque (2n + 20) / (n + 5) = (2 (n + 5) + 10) / (n + 5) = 2 + ( 10 / (n + 5)) y entonces n + 5 tiene que dividir a 10.
El truco es lograr que aparezca arriba lo que hay abajo.
¿Qué hacemos con (21 n + 4) / (14 n + 3) ?
Podemos hacer algo parecido: (21 n + 4) / (14 n + 3) = ( (14 n + 3) + (7 n + 1) ) / (14 n + 3) = 1 + (7 n + 1) / (14 n + 3).
Ahora no nos piden que sea entero, sino que tenemos que probar que es irreducible. Pero es parecido. Si la fracción original es reducible, también lo va a ser (7 n + 1) / (14 n + 3). ¿Por qué? Pensalo y escribinos si te sale.
Entonces, queremos ver si (7 n + 1) / (14 n + 3) puede ser reducible.
Puedo seguir reduciendo de esta forma, pero se pone un poco complicado. Vamos a cambiar el enfoque:
Ver si es reducible es lo mismo que ver si hay algún numero que divida a 7 n + 1 y a 14 n + 3.
Supongo que
Ahora puedo, multiplicar, sumar y restar las expresiones:
En la primera, si multiplico por 2, obtengo que p divide a 14 n + 2
¡Ahora ya casi está! Falta muy poquito, y se los dejamos a ustedes. Por favor, escriban si les sale o si no les sale.
Pero casi les contamos todo el problema :(
Bueno, para compensar vamos a ver el problema que encontró Pablo:
|
Acá terminamos por ahora, y esperamos sus mails para seguir avanzando. Tal vez los problemas de esta clase sean muy avanzados, pero no se preocupen. Manden los problemas que quieran que comentemos de cualquier nivel, ¡que nos gustan todos! ¡Será hasta la próxima!
Escriban a problematica@oma.org.ar
| OmaNet - Educación Interactiva www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |