

Nota 2 - 03 / 08 / 1999
Esperamos sus mails en problematica@oma.org.ar
En esta nota, vamos a comentar los problemas de primer nivel del certamen regional de la XV Olimpíada Nacional de Matemática.
| XV Olimpíada Nacional - Certamen Regional - Primer nivel - Problema 1 |
| Diremos que un
número natural es optimista si sus cifras
están ordenadas en forma creciente y diremos que un
número natural es pesimista si sus cifras
están ordenadas en forma decreciente. Por ejemplo, son
optimistas 1358, 24, 89, son pesimistas 41, 820, 762, y
no son ni optimistas ni pesimistas 7, 1134, 253, 9773,
8592. Hallar el primer número natural a, mayor que 150 y tal que desde 1 hasta a (inclusive) haya la misma cantidad de números pesimistas que de números optimistas. |
Existen varias formas de hacer este problema. La que vamos a dar ahora, tal vez no sea la más directa, pero usa ideas muy lindas.
Primero, empecemos probando si encontramos algún número de 3 cifras que cumpla la condición del problema; si no lo encontráramos, tendríamos que probar con otros más grandes.
Miremos que pasa con el número 999. Si tenemos un número pesimista de 3 cifras y menor que 999, al darlo vuelta obtengo un numero optimista de 2 o 3 cifras. Es decir, si doy vuelta el 754, que es pesimista, obtengo 457, que es optimista. Si doy vuelta el 621, que es pesimista, obtengo 126, que es optimista. Si doy vuelta el 540, que es pesimista, obtengo 45, que es optimista.
Es decir: por cada numero pesimista de 3 cifras, puedo encontrar uno optimista de 2 o 3 cifras. Pero ¡cuidado!, no puedo contar con este método para decir que hay la misma cantidad de optimistas que pesimistas, ya que dando vuelta números pesimistas de 2 o 3 cifras, puedo obtener el mismo número. Por ejemplo, tanto 630 como 63 son pesimistas, y al darlos vuelta, en ambos casos obtengo el 36, que es optimista.
Lo que sí puedo asegurar, es que existen tantos pesimistas de 3 cifras como optimistas de 2 o 3 cifras. Miremos ahora cuántos son los pesimistas de 2 cifras. No son tantos, así que podemos contarlos; hay 45 ( 10, 20, 21, 30, 31, 32, ..., 93, 92, 91 y 90). Por lo tanto, entre 1 y 999 inclusive hay 45 números pesimistas más que números optimistas.
Para solucionar esto, podemos intentar eliminar los últimos 45 números pesimistas, sin eliminar ningún optimista. Para ello, tengamos en cuenta que el último número optimista de 3 cifras es el 789. Si hubiera 45 números pesimistas mayores, los eliminamos y listo. Para eso, empecemos a contar los números pesimistas de atrás para adelante.
Que empiecen con 9, hay 36 (987, 986, 985, 984, 983, 982, 981, 980, 976, 975, ... , 921, 920, 910). Falta eliminar 9 más. Entonces, miramos cuáles son los últimos pesimistas que empiezan con 8: 876, 875, 874, 873, 872, 871, 870, 865 y 864.
Listo: si consideramos a = 863, hay entre 1 y a inclusive tantos optimistas como pesimistas. Ahora tenemos que ver que no haya otro número más chico que también cumpla la condición del problema.
Les dejamos esa parte para ustedes. ¿Pueden hacerlo? ¿Alguien consiguió otra solución?
| XV Olimpíada Nacional - Certamen Intercolegial - Primer nivel - Problema 2 |
| En el trapecio ABCD, de bases AB y CD, y lados BC y AD, AD = 39, CD = 14, ángulo ABC = 69° y ángulo CDA = 138°. Hallar la medida de AB. |
El gran truco acá es trazar alguna segmento adicional. Por ejemplo, agregamos un segmento CE con E en AB y CE paralelo a AB.
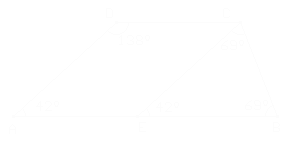
¡Epa! Eso fue demasiada ayuda... Sigan solos, por favor.
| XV Olimpíada Nacional - Certamen Intercolegial - Primer nivel - Problema 3 |
| En cada vértice de un cuadrado
hay una semilla. Una hormiga sale de un vértice y camina
por los lados del cuadrado arrastrando una enorme bolsa
de semillas y sólo se detiene en los vértices. Cuando
llega a un vértice, si viajaba en el sentido de las
agujas del reloj, agrega tantas semillas como las que hay
en el vértice del que venía, y si viajaba en sentido
contrario a las agujas del reloj, quita semillas, agrega
semillas, o no hace nada, de modo que quede la misma
cantidad que en el vértice del cual venía. ¿Puede la hormiga organizar su viaje para tener exactamente 98 semillas en cada vértice? Si la respuesta es no, explicar por qué. Si la respuesta es sí, indicar el camino de la hormiga. |
Sí, ¡¡se puede!! Vamos a ver una forma:
Llamemos A, B, C y D a los vertices del cuadrado en sentido horario. Si la hormiguita, sin pensarlo, se pusiera a caminar en este sentido, partiendo del vértice A, ocurriría lo siguiente:
| A | B | C | D | |
| Inicialmente | 1 semilla | 1 semilla | 1 semilla | 1 semilla |
| 1ra vuelta | 1 semilla | 2 semillas | 3 semillas | 4 semillas |
| 2da vuelta | 5 semillas | 7 semillas | 10 semillas | 14 semillas |
| 3ra vuelta | 19 semillas | 26 semillas | 36 semillas | 50 semillas |
| 4ta vuelta | 69 semillas | 95 semillas | 131 semillas | ... |
Vemos que de esta manera no se obtienen las 98 semillas en ningún vértice. No obstante, lo que la hormiga sí puede hacer, es en un determinado momento, dar una vuelta entera en sentido antihorario, de manera que en todos los vértices quede una misma cantidad de semillas, a la que podemos llamar, por ejemplo, X (X deberá ser alguno de los números de semillas que aparecieron arriba). A partir de ese momento, si vuelve a empezar a dar vueltas en sentido horario, ocurre algo similar a lo que ocurrió al principio. (como si cada grupito de X semillas fuera una sóla semilla):
| A | B | C | D | |
| Después de la vuelta al revés | X semillas | X semillas | X semillas | X semillas |
| 1ra vuelta | 1 X semilla | 2 X semillas | 3 X semillas | 4 X semillas |
| 2da vuelta | 5 X semillas | 7 X semillas | 10 X semillas | 14 X semillas |
| 3ra vuelta | 19 X semillas | 26 X semillas | 36 X semillas | 50 X semillas |
| 4ta vuelta | 69 X semillas | 95 X semillas | 131 X semillas | ... |
Entonces, lo que podemos hacer, es ver si ahora podemos llegar a dejar 98 semillas en algún vértice. Para eso, 98 debería poder escribirse como un múltiplo de X de los que aparecen arriba. Recordemos además, que X es una cantidad de semillas que haya aparecido en el primer recorrido de la hormiga.
Esto nos da una idea de que podemos factorizar 98 y ver si sus divisores aparecen entre las cantidades de semillas que van apareciendo en los vértices en el primer recorrido que sugerimos para la hormiga. En efecto, 98 = 2 . 7 . 7 = 7 . 14, por ejemplo. Entonces, podemos hacer que X sea 7. En la tercera vuelta, al llegar a D, tendremos 14X = 14 . 7 = 98 semillas en ese vértice.
En definitiva, el movimiento de la hormiga podría ser; por ejemplo, el siguiente:
| A | B | C | D | |
| Inicialmente | 1 semilla | 1 semilla | 1 semilla | 1 semilla |
| 1ra vuelta | 1 semilla | 2 semillas | 3 semillas | 4 semillas |
| 2da vuelta | 5 semillas | 7 semillas |
Y al llegar a B da una vuelta y cuarto al revés en sentido anithorario, volviendo a A, y dejando todos los vértices con 7 semillas. Luego, vuelve a empezar.
| A | B | C | D | |
| Después de la vuelta al revés | 7 semillas | 7 semillas | 7 semillas | 7 semillas |
| 1ra vuelta | 7 semilla | 14 semillas | 21 semillas | 28 semillas |
| 2da vuelta | 35 semillas | 49 semillas | 70 semillas | 98 semillas |
Al llegar a este punto, nuevamente, da una vuelta en sentido antihorario, para que queden 98 semillas en cada vértice.
Pero como ya dijimos, hay muchos otros caminos. Así que pueden buscarlos.
| OmaNet www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |