

Clase 4 - Test de paridad
La idea del test de paridad es realmente sencilla y consiste en que un número impar no se puede obtener como suma de números pares. Aunque se trata de un enunciado verdaderamente simple los problemas que utilizan esta idea no lo son tanto.
La razón de esto es que no siempre es evidente que hay que aplicar el test de paridad. En varios problemas donde hay que decidir si algo es o no posible hay alguna cosa que permanece invariante y es cosa muchas veces es la paridad. A lo largo de esta clase iremos viendo distintos problemas donde subyace oculta la paridad a modo de un pantallazo general sobre como aplicar este test.
Problema 1: Se tiene escrito sobre un pizarrón once números 1. Una posible operación es tomar dos números y sumarle a ambos 1, restarle a ambos 1 ó sumarle a uno de los números 1 y restarle 1 al otro. ¿Es posible mediante estas operaciones tener escritos en el pizarrón once números 10?
Solución: Al sumar a ambos números 1, la suma de todos los números aumenta en 2; al restar a ambos números 1, la suma total disminuye en 2; y al sumarle 1 a un número y restarle 1 al otro, la suma total no se ve afectada.
Como consecuencia de esto, dado un conjunto de números iniciales, al efectuar repetidas operaciones, la paridad de la suma total no cambia. Es decir, que si la suma de todos los números al principio era impar, al final también será impar pues las operaciones lo único que hacen es sumar +2, 0 ó -2 a la suma total.
En nuestro ejemplo la suma de todos los números al principio es 11 y al final 110. Como vemos estos números no tienen la misma paridad (uno es par y el otro impar) y por tanto no se puede llegar a tener once números 10.
¿Se animan a encontrar todos los posibles resultados finales a lo que se puede llegar a través de las operaciones permitidas?¿Pueden dar una sucesión de operaciones para que partiendo de once números 1 se llegue a once números 3?
Problema 2: ¿Tiene la siguiente ecuación soluciones en enteros x³ + 7x + 14549535 = 0?
Solución: Una aproximación ingenua al problema consistiría en utilizar el teorema de Gauss para polinomios. ¿Recuerdan que el año pasado vimos que si un polinomio de coeficientes enteros tiene raíces racionales de la forma p/q (con p y q coprimos), entonces p divide al término independiente y q divide al coeficiente principal?
En este caso si el polinomio tiene raíces racionales entonces, éstas serán enteras (pues el coeficiente principal es 1) y deberán dividir a 14549535 = 32.5.7.11.13.17.19. Sin embargo, este número tiene 384 divisores, lo que haría el trabajo muy tedioso.
Veamos como el test de paridad nos facilita mucho nuestro trabajo. Si x es impar: x³ es impar (porque cualquier potencia de un número impar es impar), 7x es impar, y 14549535 es impar. Por lo tanto, como la suma de tres números impares es impar entonces x³ + 7x + 14549535 no puede valer 0 (pues es par).
En el caso de que x sea par: x³ es par (porque cualquier potencia de un número par es par), 7x es par pues x era par, y 14549535 es impar. Por lo tanto, como la suma de dos números pares y uno impar, es impar entonces x³ + 7x + 14549535 no puede valer 0 (pues es par).
En conclusión la ecuación x³ + 7x + 14549535 = 0 no tiene soluciones en enteros. De hecho, tampoco tiene soluciones en racionales. ¿Se animan a probar que tiene una raíz irracional y dos raíces complejas?
Problema 3: Se quiere cubrir el siguiente tablero con fichas de dominó (que ocupan dos casilleros). Demostrar que no es posible hacerlo.

Solución: Un primer intento para atacar este problema podría ser contar los casilleros y fijarse si la cantidad es par o impar. Si la cantidad fuera impar el problema ya estaría solucionado pues cada ficha de dominó abarca dos casilleros por lo que un tablero cubierto con fichas de dominó debe tener siempre una cantidad par de casilleros. Lamentablemente, este no es el caso porque la cantidad de casilleros es 28, que es par.
Por tanto, hay que adoptar otra estrategia. Si coloreamos el tablero de blanco y negro como un tablero de ajedrez, notamos que hay 15 casillas negras y 13 blancas.
 |
Ahora bien, una ficha de dominó ubicada en cualquier lugar del tablero tapa una casilla blanca y una casilla negra. Por tanto, nunca podremos cubrir todo el tablero con fichas de dominó ya que no hay igual cantidad de casillas blancas que de negras. |
La idea de pintar un tablero de blanco y de negro resulta de gran utilidad a la hora de resolver problemas ya que permite en muchos casos hallar ese algo invariante del que hablábamos al comienzo de la clase. Otras veces no alcanza con pintar el tablero con dos colores por lo que se puede extender esta idea pintándolo de tres, cuatro o más colores.
Problema 4: En un tablero de 4x4 Pedro y Martín se turnan para colocar ceros o unos en cada casillero. Pedro gana si la suma de los números de alguna fila es impar. De lo contrario gana Martín. Comienza jugando Pedro, ¿quién tiene la estrategia ganadora? Por qué.
Solución: Una posible objeción al enunciado del problema es que supone de antemano que alguno de los dos jugadores tiene la estrategia ganadora (es decir una serie de jugadas que le aseguran ganar independientemente de lo bien que juegue su contrario). De hecho esto es cierto por que "En todo juego donde no interviene el azar y no hay posibilidad de empate siempre alguno de los jugadores tiene la estrategia ganadora".
Veamos que Martín tiene la estrategia ganadora. Comienza Pedro escribiendo un número en cualquier casillero. En la misma fila Martín escribe en otro casillero el mismo número que escribió Pedro. Luego Pedro escribe otro número y Martín escribe en la misma fila el mismo número que Pedro escribió. Y así siguen sucesivamente.
Martín siempre puede escribir un número en la misma fila que escribió Pedro, pues cuando Pedro escribe un número en una fila, ésta tenía escritos o bien ningún número o dos números (uno escrito por Pedro y el que escribió Martín según su estrategia) y como las filas tienen 4 casilleros Martín siempre puede aplicar su estrategia de escribir en la misma fila el mismo número que escribió Pedro en su turno anterior.
De este modo, Martín se asegura que la suma de la fila sea par (ya que habrán todos ceros, dos ceros y dos unos, o todos unos) y por lo tanto gana.
Fíjense que el problema no cambiaba si el tablero era de 100x100 o de 1000x708 porque lo que importaba es que las filas tuvieran una cantidad par de casilleros para poder aplicar la estrategia de Martín.
Cabe destacar que, en la mayoría de los casos, el test de paridad no nos proporciona la estrategia que deben utilizar los jugadores (en el caso de un juego). Del mismo modo, en los problemas con tableros o en los de números naturales el test de paridad sirve para ver porque algo no puede suceder, pero en caso de que pueda, no nos da la forma de solucionar el problema.
Supongamos que en el problema de las fichas de dominó la cantidad de casilleros blancos fuera igual que la cantidad de negros el test de paridad no indica como ubicar las fichas. Por tanto, generalmente se usa paridad para demostrar que una situación no se puede dar.
Como habrán visto el test de paridad permite resolver una cantidad infinita de problemas de diversa índole, ya sea ecuaciones, tableros, juegos, problemas con número enteros, y más. A continuación les dejamos algunos problemas para que resuelvan, aunque lamentablemente la idea más importante ya está dada: hay que usar paridad.
Problemas
1. Se tienen triángulos rectángulos de catetos 3 y 4. Con algunos triángulos se forma un cuadrado. Demostrar que para que esto sea posible la cantidad de triángulos utilizados debe ser par.
2. ¿Puede ser la suma de 10 naturales consecutivos igual a 11111?
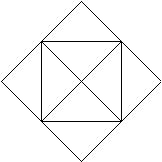
3. Decidir si es posible recorrer la figura con un lápiz sin levantar el lápiz del papel y sin pasar dos veces por el mismo segmento.
4. Sea f:N-->N tal que:
¿Existe algún valor de n tal que (1 + 2 + ... + n) + (f(1) + f(2) + ... + f(n)) = 100n+1?
5. Se tiene el siguiente tablero de ajedrez y un caballo. Colocando el caballo en cualquier casillero se pretende que, por medio de los movimientos correspondientes al caballo, pase por todos los casilleros del tablero una y sólo una vez. ¿Es esto posible? De ser así, mostrar el recorrido del caballo, de lo contrario justificar.
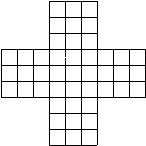
6. A una fiesta concurre una cierta cantidad de personas. Probar que siempre la cantidad de personas que saluda a una cantidad impar de personas, es par.
7. Se dispone de un tablero de ajedrez (8×8) y de una ficha. Los movimientos permitidos para la ficha son:
Si al intentar avanzar los 3 casilleros en alguna de estas direcciones se llega a un borde, entonces se debe completar el movimiento retrocediendo las casillas necesarias en esa dirección o utilizando otra dirección. Hallar el menor número de movidas necesarias para llegar desde la casilla inferior izquierda hasta la casilla superior derecha.
8. Un juego consiste de 9 botones luminosos (de color verde o rojo) dispuestos formando un cuadrado de 3×3. Si se aprieta un botón del borde cambian de color él y todos sus vecinos, y si se aprieta el botón del centro cambian de color todos sus vecinos pero él no. ¿Es posible (apretando sucesivamente algunos botones) encender todas las luces con color verde, si inicialmente estaban todas encendidas con luz roja? Justifique la respuesta.
Esta fue la cuarta clase de Miscelánea 2001, el curso de matemáticas por Internet. Esperamos que les haya gustado. En quince días, ofreceremos una nueva clase.
Ahora, es el turno de ustedes. Queremos que hagan los problemas y ejercicios que fuimos dando a lo largo de la clase. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es misc@oma.org.ar .
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
| Internet vía OmaNet www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |