Clase 1 - Función cuadrática

Esperamos sus mails en misc@oma.org.ar

En esta primer clase de Miscelánea veremos algunos temas y problemas relacionados con la función cuadrática. Por si no lo recuerdan, una función cuadrática es una función tal que
f(x) = ax² + bx + c y su representación gráfica es una parábola. Aquí van los problemas...

A. Se tienen dos funciones cuadráticas f(x) = x²+kx+p y g(x) = x²+px+k distintas entre sí que tienen una raíz en común. Hallar el valor de dicha raíz y el valor de p+k.

B. Sea f(x) = x²+a y sea g(x) = -2x²+ax. Hallar los valores de a para que ambas funciones sean tangentes.

C. Se tiene un triángulo rectángulo ABC con C = 90° y tal que AC = 2 y BC = 3. Dado un punto P en AB sea R en AC de modo que RP es perpendicular a AC y sea Q en BC de modo que PQ sea perpendicular a BC. Hallar la medida de los lados del rectángulo RPQC sabiendo que éste tiene área máxima.

D. Sea (x_t, y_t) el vértice de la parábola y = 2x² + tx +1. Hallar el lugar geométrico de dichos puntos para t variando en los números reales.

¿Pudieron hacerlos? De todas formas veremos más adelante las soluciones. Mientras tanto repasemos primero algunos temas que serán útiles para la resolución de los ejercicios.

Como sabrán la función cuadrática tiene siempre dos raíces, aunque no siempre sean reales o distintas entre sí, llamémoslas x₁ y x₂ . Por tanto, la función cuadrática también se puede representar como f(x) = a (x - x₁)(x - x₂) = ax² - a(x₁+x₂)x + ax₁x₂ .

Comparando esta forma de representar la función con la que dimos al principio podemos ver que la suma de las raíces de f(x) es igual a -b/a y el producto de dichas raíces es c/a. Saber el valor de la suma de las raíces de f(x) nos sirve para hallar el eje de simetría de la parábola, pues fíjense: f(-b/2a+x) = f(-b/2a-x) = ax² - b²/4a + c. Por lo tanto, el eje de simetría tendrá ecuación x = -b/2a.

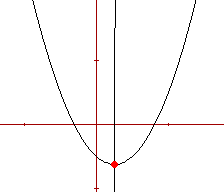
Sobre este eje de simetría se encontrará el máximo de la función (si el coeficiente a es negativo) o el mínimo (si a es positivo). Es decir que f(-b/2a) será el mayor o el menor valor que tome la cuadrática. Dicho punto se llama vértice de la parábola.

Volviendo a una cuestión pendiente del principio, ¿cuándo tiene una función cuadrática dos, una o ninguna raíz real? ¿Recuerdan la fórmula de las raíces de la ecuación cuadrática?

Bueno, basándonos en esta fórmula podemos saber cuántas raíces reales tiene la función. Si b²-4ac (este número se llama discriminante) es positivo, entonces habrá dos raíces reales. ¿Por qué? En el caso de que b²-4ac sea cero tendremos que las dos raíces reales coinciden, o dicho de otro modo tiene una raíz doble. En este caso la parábola es tangente al eje de las abscisas (el eje de las x). Finalmente si b²-4ac es negativo, como la raíz de un número negativo da un número complejo, entonces la función no tendrá raíces reales.

Con todo esto ya estamos en condiciones de resolver los problemas que propusimos. Antes de leer las soluciones, si no les salieron antes, intenten hacerlos nuevamente.

Soluciones

A. Supongamos que a y b son las raíces de f(x) y que las raíces de g(x) sean a y c (a es la raíz común a ambas cuadráticas). Entonces f(x) = x² - (a+b)x + ab y g(x) = x² - (a+c)x + ac.

Como el coeficiente de x en f(x) es igual al término independiente de g(x) entonces -a - b = ac. Del mismo modo sabemos que -a -c = ab. Restemos ambas ecuaciones: c - b = a (c-b).

Para poder cancelar c-b a ambos lados debemos probar que c-b es distinto de cero, o lo que es lo mismo que b es distinto de c. ¿Qué pasaría si c-b fuera cero? Los valores de c y b no pueden ser iguales pues de lo contrario f(x) y g(x) serían la misma función porque tendrían las mismas raíces y el mismo coeficiente de x². Por tanto, podemos cancelar y queda que 1 = a. Es decir que la raíz que f(x) y g(x) tienen en común es 1.

En f(x) tenemos que k+p = -(a+b) + ab. Reemplazando el valor de a obtenido, entonces llegamos a que k+p = - 1 - b + b = -1.

B. Que ambas funciones cuadráticas sean tangentes significa que se tocan en un sólo punto y que además f(x) > g(x) para todo x. Las funciones se intersecan en un sólo punto si la ecuación:
x² + a = -2x² + ax tiene una sola raíz. Es decir, que el discriminante de 3x² - ax + a = 0 debe ser igual a cero. Entonces a² - 12a = 0 donde a = 0 ó a = 12.

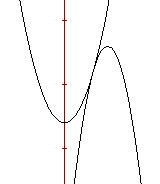
Veamos el caso de a = 12. Ya sabemos que f(x) = x² + 12 y g(x) = -2x²+12x se tocan en un punto. Veamos que x² + 12 > -2x²+12x, o lo que es lo mismo x² - 4x + 4 = (x-2)² > 0, lo cual es cierto pues el cuadrado de un real siempre es positivo. El caso de a = 0 se lo dejamos a ustedes.

C. Hagamos una figura para ver mejor las cosas:

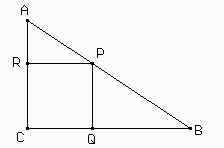
Si CQ = x entonces QB medirá 3-x. Debido a que PQ // AC los triángulos PQB y ABC son semejantes de donde PQ / AC = QB / BC. Reemplazando los datos ya conocidos tenemos que PQ / 2 = (3-x) / 3, o lo que es lo mismo: PQ = (6-2x)/3.

El área del rectángulo RPQC es igual a CQ . PQ = x.(6-2x)/3 = f(x). Calculemos el máximo de esta función (tiene máximo pues el coeficiente principal es negativo). Las raíces de f(x) son x = 0 y x = 3, por lo que el eje de simetría está en x = 1,5, mismo lugar donde se halla el máximo. Por tanto para que el área de RPQC sea máxima CQ = 1,5 y PQ = 1.

D. El promedio de las raíces de la parábola es igual a -t/4, es decir que x_t = -t/4. Entonces
y_t = 2.(-t/4)² + t (-t/4) + 1 = -t²/8 + 1. Por lo tanto el vértice de la parábola será (-t/4, -t²/8+1).

Buscamos la relación que vincula estas coordenadas. Si x = -t/4 entonces -4x = t. Reemplazando en la ecuación de y_t tenemos que y_t = -2x² + 1.

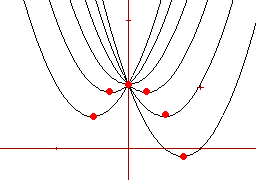
Por lo tanto, el lugar geométrico de dichos puntos es la parábola de ecuación y = -2x² + 1.

Para terminar esta clase, les dejamos algunos ejercicios para que practiquen. Cualquier duda que tengan, o si quieren mandarnos alguna solución a la que llegaron no duden en escribirnos.

Problemas

1. Demostrar la fórmula de las raíces de la ecuación cuadrática.

2. Sea f(x) = x²+ax+b con raíces p y q; y sea g(x) = x²+cx+b una función cuadrática con raíces p+1 y q+1. Hallar los valores de a y c.

3. Los lados de un triángulo rectángulo cumplen la siguiente condición: el promedio de los tres lados es igual a uno de ellos. Hallar la razón entre los lados del triángulo.

4. Se sabe que para la función cuadrática f(x), f(3) = f (1). Si 5 es una raíz, ¿cuál es la otra? ¿Cuál es la función?

5. Sea f(x) = -x²+2. Hallar un punto P de la función en el primer cuadrante de modo que el rectángulo que tiene a P y al origen de coordenadas como vértices opuestos, y que se apoya sobre el eje x y sobre el eje y, tenga perímetro mínimo.

6. Dada la recta de ecuación y = 2x +1 y f(x) = ax²+ax+2. Hallar los valores de a para los cuales la recta y la parábola son tangentes.

7. Demostrar que, sin importar los valores de a y b (con a distinto de b), la función f(x) = 2x² + (2a+2b)x + a² + b² no tiene raíces reales.

Esta fue la primer clase de Miscelánea, el curso de matemáticas por Internet. Esperamos que les haya gustado. En quince días, ofreceremos una nueva clase.

Ahora, es el turno de ustedes. Queremos que hagan los problemas y ejercicios que fuimos dando a lo largo de la clase. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es misc@oma.org.ar .

Miscelánea OmaNet	OmaNet - Educación Interactiva    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar