Clase 15 - Traslación de ángulos

Esperamos sus mails en educabri@oma.org.ar.

 

Ya vimos cómo trasladar segmentos. Vamos a aprender ahora a trasladar ángulos

Parte 1. Actividades

Trasladar un ángulo es más difícil que trasladar segmentos, y se pueden hacer distintas construcciones. Vamos a ver una. Te sugerimos que pienses como podrías hacerlo antes de seguir o que busques nuevas formas de hacerlo.

1-1 Traslación de ángulos

1. Creá tres puntos y llamalos A, B y C. Trazá los segmentos AB y BC.
2. Creá un segmento QR.

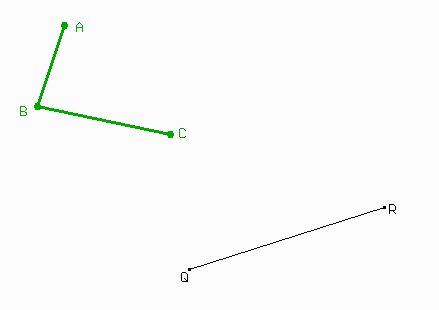
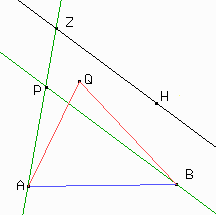
Lo que queremos hacer es trazar una recta r por Q tal que el ángulo que forme con QR sea igual al ángulo ABC.

3. Trazá una recta s paralela a BA por Q y una recta t paralela a BC por Q. Tomá dos puntos S y T en s y t respectivamente.

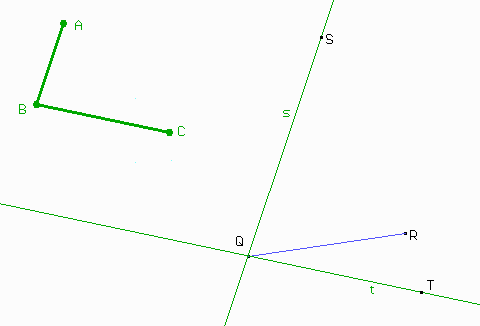
Eso no es exactamente lo que queremos. Nos gustaría ahora apoyar el ángulo sobre el lado QR. Imaginemos que trazamos la recta r buscada. Como los ángulos PQR y SQT son iguales, resulta que los ángulos PQS y RQT también son iguales..

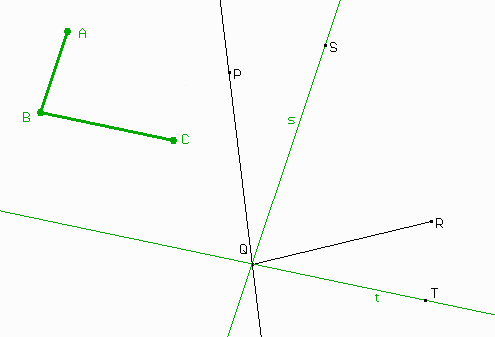
Ahora, ¿cómo podemos usar eso para trazar la recta r?

4. Trazá la bisectriz de SQR. Llamá z a esa recta y toma un punto Z sobre ella.

Fijate que los ángulos TRZ y SRZ también deben ser iguales. Entonces:

5. Trazá el punto simétrico de T con respecto a la bisectriz recién trazada.
6. Llamá P a este punto y trazá la recta PQ. ¡Esa es la recta que buscábamos!

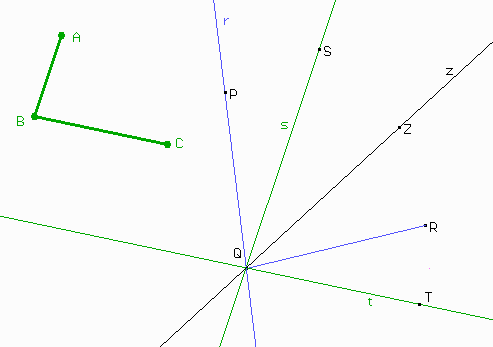
¿Se entendió lo que hicimos?

7. Ocultá los objetos auxiliares. Medí los ángulos ABC y PQR y mové los puntos para ver que siempre se cumple lo que queríamos.

1-2 Una nueva mirada al arco capaz

Cuando en la clase 9 construimos un arco capaz, usamos lo que ya sabíamos: que iba a ser un arco de circunferencia.

Ahora que sabemos trasladar ángulos, podemos construir el arco capaz sin saber eso. Entonces, vamos a resolver con el Cabri:

"Dado un segmento AB y un punto Q hallar el lugar geométrico de todos los puntos P tales que los angulos AQB y APB son iguales."

1. Creá un segmento AB y tomá un punto Q fuera de él.
2. Creá un punto básico Z y trazá la recta AZ.

Queremos encontrar un punto P sobre la recta AZ tal que APB = AQB.

3. Trasladá el ángulo AQB sobre AZ. Es decir, encontrá un punto un punto H tal que AZH = AQB
4. Trazá una recta por B paralela a ZH.
5. Marcá P en la intersección de esta última recta y la recta AZ.
6. Medí los ángulos APQ y ABQ. Justificá por qué funciona todo lo que hicimos. (Depende como hayas hecho la construcción puede ser que el ángulo APQ cambié al cambiar Z de semiplano, pero eso no es muy importante...)

Con esto ya podemos el lugar geométrico:

7. Ocultá los objetos auxiliares y construí el lugar geométrico de P al mover Z sobre el plano. ¡Excelente!

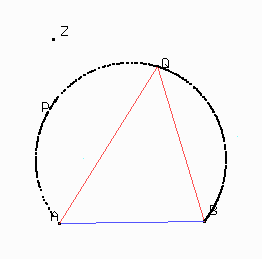
Parte 2. Problemas

2-1 Construir un triángulo dados dos lados y el ángulo comprendido..

2-2 Dado un cuadrilátero ABCD y dos puntos PQ, trasladar el cuadrilátero de forma que A coincida con P y B esté en la recta PQ.

Así terminamos la decimoquinta clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar