Clase 13 - Más sobre el lugar geométrico

Esperamos sus mails en educabri@oma.org.ar.

 

Como dijimos en la clase 12, vamos a aprender a usar los lugares geométricos para resolver algunos problemas donde no se pide explicitamente encontrar un lugar geométrico.

Parte 1. Actividades

¿Resolviste el problema 4 de la clase 12? Ese problema apareció en la III Olimpíada del Cono Sur, y muy pocos encontraron la elegante solución que ofrecemos ahora.

Si todavía no lo pensaste, te recomendamos que le dediques un tiempo antes de seguir.

• Dada una circunferencia y un punto P fuera de ella, encontrar dos puntos Q y R en la circunferencia tales que P, Q y R estén alineados y Q sea el punto medio del segmento PR.

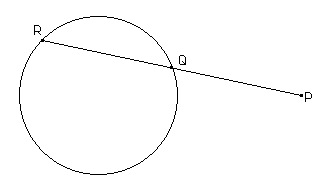
Podemos re-escribir el problema así:

• Dada una circunferencia y un punto P fuera de ella, encontrar un punto Q sobre la circunferencia tal que si R es el simétrico de Q con respecto a P, entonces R esté sobre la circunferencia.

Así, debemos encontrar un punto Q con dos propiedades:

1. Q está sobre la circunferencia.
2. El simétrico de P con respecto a Q está sobre la circunferencia.

Acá entra lo de lugar geométrico.

1. ¿Cuál es el lugar geométrico de los puntos que cumplen i.? ¡Esta es fácil!
2. ¿Cuál es el lugar geométrico de los puntos que cumplen ii.? ¡Esta no es tan fácil! (Acá no nos interesa que Q esté sobre la circunferencia. Buscamos los puntos del plano tales que el simétrico esté sobre la circunferencia.)

Ahora, si sabés cuáles son los puntos que cumplen i. y cuáles son los puntos que cumplen ii., ¿cuáles serán los puntos que cumplan ambas cosas a la vez? La respuesta viene dada por la siguiente propiedad obvia, pero muy útil:

Si D es el lugar geométrico de los puntos con una cierta propiedad y E es el lugar geométrico de los puntos con otra cierta propiedad, el lugar geométrico de los puntos que cumplen ambas propiedades simultáneamente es la intersección entre D y E.

Para que no queden dudas, resolveremos la segunda pregunta:

Decir que R es el simétrico de Q con respecto a P es equivalente a decir que Q es el punto medio de PR. Entonces, dado un punto R en la circunferencia, podemos tomar el punto medio Q. Al mover el punto R sobre la circunferencia, obtendremos todos los puntos Q que cumplen lo que queremos.

3. ¿Cuál es el lugar geométrico del punto medio de PR al mover R sobre la circunferencia? (Esta es la misma pregunta que hicimos en la clase 0.)
4. Trazá este lugar geométrico y marcá la intersección entre las dos circunferencia. Llamá a los puntos obtenidos Q₁ y Q₂. (Dependiendo de la posición de P, puede haber 0, 1 o dos puntos de intersección.)
5. Construí los simétricos R₁ y R₂. Estos dos pares de puntos son las soluciones del problema.

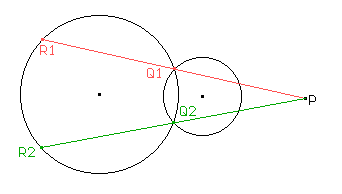
¿Se entendió? Recomendamos hacer los problemas que vienen a continuación para agarrarle la mano a todo esto.

Parte 2. Problemas

2-1 Sean r y s dos rectas no paralelas y sea P un punto que no pertenece a ninguna de las rectas. Encontrar puntos A y B sobre las rectas r y s, tales que P sea el punto medio de AB.

2-2 Sean C y D dos circunferencias, que se intersecan en los puntos A y B. Hallar puntos P y Q sobre C y D respectivamente, tales que A sea el punto medio de PQ.

2-3 Dado un cuadrado ABCD y un punto P sobre AB, construir un triángulo equilátero PQR tal que Q esté sobre BC y R sobre CD. ¿Para qué puntos es posible la construcción?

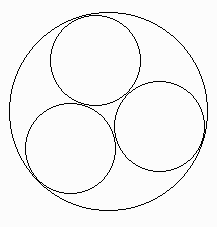
2-4 Dada una circunferencia C, inscribir tres circunferencias mutuamente tangentes, y tangentes a C, como se ve en la figura.

Así terminamos la decimotercera clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar