Clase 12 - Lugar Geométrico

Esperamos sus mails en educabri@oma.org.ar.

 

Ya hablamos muchas veces de lugares geométricos. En la clase 0, vimos como usar el comando locus of points para construir un lugar geométrico y en la última clase hallamos un lugar geométrico más complicado.

En esta clase vamos a ver mejor de que se trata eso.

Parte 1. Actividades

Empecemos con un problema, parecido al de la clase 0.

1. Trazá una recta básica r, un punto P fuera de ella y un punto Q sobre la recta.
2. Trazá el segmento PQ y construí el punto medio de PQ, que llamaremos M.
3. Mové el punto Q por la recta r. ¿Qué figura describe M al mover Q?

En este caso, resulta fácil contestar la pregunta. A veces, descubrir que figura describe un punto no es tan fácil. Para eso, existe el comando Locus of points del Cabri.

4. Construí el lugar geométrico de M al mover Q, usando el comando Locus of Points.
5. ¿Qué se obtiene?

Si todo salió bien, habrás obtenido una recta. Esta recta es el "lugar geométrico" de M al mover Q.

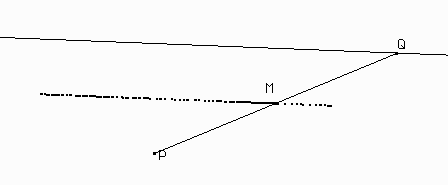
En general, llamamos lugar geométrico de un punto M al variar otro punto Q sobre un objeto como el conjunto de posiciones que toma M al mover Q sobre ese objeto.

El Cabri nos ayuda a intuir un lugar geométrico. ¡Pero no hay que conformarse con eso! Tenemos que determinar con precisión lo que observamos y demostrarlo:

6. ¿Cómo son las dos rectas en el dibujo?
7. ¿Qué relación hay entre la distancia de P a la recta r y de P a la otra recta?

El lugar geométrico es la recta paralela a r, tal que la distancia de ella a P es la mitad de la distancia de r a P. Llamaremos s a esta recta. Demostrar que s es efectivamente el lugar geométrico tiene dos partes:

• Probar que si un punto pertenece al lugar geométrico, entonces está en s.
• Probar que todos los puntos de s forman parte del lugar geométrico. Es decir, que para cualquier punto M' que tomemos en s, existe un punto Q' en r tal que M' es el punto medio de PQ'

Para la primera parte, vamos a necesitar el teorema de Thales. Veremos mejor este teorema más adelante. Por ahora simplemente lo enunciaremos.

8. Tomá un punto Q₁ en r tal que PQ1 sea perpendicular a r y un punto cualquiera Q₂ en r.
9. Construí los puntos medios correspondientes: M₁ y M₂.
10. Claramente, M₁ está en s, por la forma en que construimos s.

Queremos ver que M₂ también está en s. El teorema de Thales nos dice que si QM₁ / M₁P = QM₂ / M₂P, entonces la recta M₁M₂ resulta paralela a r.

11. Calculá QM₁ / M₁P y QM₂ / M₂P.
12. Deducir que M₂ pertenece a s, como se quería probar.

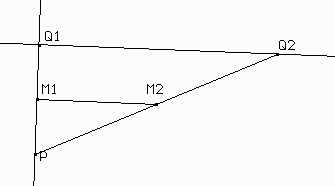
Ahora veamos la segunda parte. Tenés que tomar un punto en s y encontrar el punto en r correspondiente.

14. Construí la recta s. (Sin usar locus of points, para poder trabajar con ella.)
15. Tomá un punto M' en s.
16. Tenés que encontrar el punto Q'. ¿Se te ocurre como? Muy simple: symmetrical point.
17. Si movés el punto M', vas a ver que Q' se mueve sobre r. Pero, ya sabés, esto no es suficiente.
18. Demostrá que Q' está en r. (Sug.: ¡teorema de Thales!)

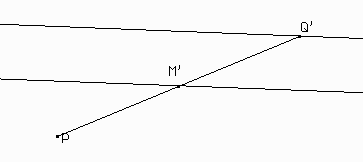
Así terminamos todos los pasos. Parece bastante largo y complicado, pero una vez que uno entiende bien lo que estamos haciendo, se logra hacer con facilidad.

Por esta semana, dejamos acá. Saber trabajar con lugares geométricos sirve para resolver muchos problemas de geometría. Y no sólo los que dicen "Hallar el lugar geométrico de ...". Eso lo veremos en la próxima clase.

Parte 2. Problemas

2-1 Son dados un triángulo ABC, y un punto P. Sea S₁ el punto simétrico de P con respecto a A, S₂ el punto simétrico de S₁ con respecto a B y S₃ el punto simétrico de S₂ con respecto a C. Hallar el lugar geométrico de S₃ al mover P.

2-2 Dados un punto P y los puntos A y B se construyen los rectángulos ABCD con P perteneciente a la recta CD. Hallar el lugar geométrico de D si B se mueve en una circunferencia de centro A.

2-3 Sea C una circunferencia de centro O y A un punto exterior a la circunferencia. Sea P un punto sobre C. Se traza la circunferencia D, de centro A que pasa por P y la recta r que pasa por O y P. La recta r corta a D en dos puntos (uno es P). Sea M el punto medio de estos dos puntos. Hallar el lugar geométrico de M al variar P sobre C.

2-4 Dada una circunferencia y un punto P fuera de ella, encontrar dos puntos Q y R en la circunferencia tales que P, Q y R estén alineados y Q sea el punto medio del segmento PR.

Así terminamos la duodécima clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar