Clase 11 - Dos problemas

Esperamos sus mails en educabri@oma.org.ar.

 

Vamos a resolver ahora dos problemas que dejamos en clases anteriores. Si todavía no los pensaron, ¡haganlo antes de leer las soluciones!

Clase 7 - Problema 3  Se tienen dados tres puntos: O, G y M. Construir un triángulo de forma tal que O sea su circuncentro, G su baricentro, y M el punto medio de un lado.

Observemos primero la figura a la que queremos llegar, para ver que cosas nos pueden servir.

1. A, G y M están alineados. Más aún, AG = 2 GM (Esto lo vimos en la clase sobre el baricentro.)
2. OM es perpendicular al lado BC.
3. A, B y C están en la circunferencia con centro O que pasa por alguno de los vértices.

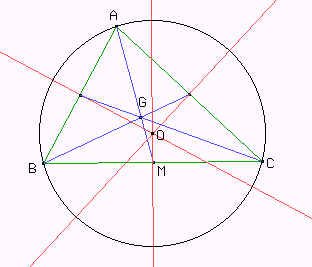
Estos tres datos nos van a servir para construir lo que nos piden:

G y M los tenemos, entonces por (1) podemos encontrar A. Construimos un punto P, simétrico de M con respecto a G y construimos A, el simétrico de P respecto a G.

Trazamos la recta OM, y la recta s, perpendicular a OM por M. Por (2), los puntos B y C van a estar sobre esta recta.

Ahora, trazamos la circunferencia con centro O que pasa por A. Por (3), los puntos B y C tienen que estar sobre esta circunferencia. Juntando esto con lo que ya sabemos, obtenemos que B y C son las intersecciónes entre esta circunferencia y la recta s.

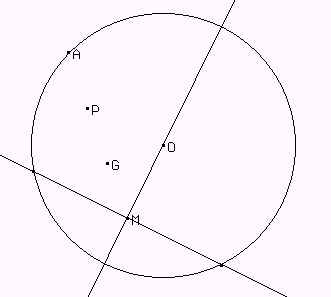
Encontramos A, B y C y tenemos nuestro triángulo.
Sólo faltaría ver que este triángulo cumple todo lo que nos piden.

Nota: tal vez les parezca que, por cómo hicimos la construcción, ya no queda nada por hacer. Pero podría haber problemas si los datos fuesen redundantes o contradictorios. De todos modos, lo que falta es muy fácil.

O es circuncentro porque los tres puntos A, B y C están sobre una circunferencia de centro O.

M es punto medio de BC, porque el triángulo BOC es isósceles (BO = CO = r) y M es el pie de la altura (OM es perpendicular a BC).

G es el baricentro, porque esta sobre el segmento AM (con M punto medio de BC) y AG = 2 AM.

Entonces se cumple todo lo pedido, y el problema queda resuelto.

Clase 10 - Problema 3. Sean A, B y C puntos sobre una circunferencia. Llamemos H al ortocentro del triángulo. Hallar el lugar geométrico de H al mover A sobre la circunferencia.

(Este problema apareció en la 2^da competencia de Clubes Cabri. La solución que sigue es esencialmente la que hicieron los clubes Ortocentro, Baricentro, Huergo, Inducción, Moro Zubillaga y Eureka en esa prueba.)

Sean E y F los pies de las alturas del ABC trazadas desde B y C respectivamente. AEH = AFH = 90° ya que las alturas por definición son perpendiculares a los lados opuestos.

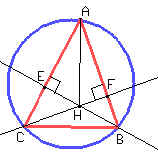
Como AEHF es un cuadrilátero, la suma de sus ángulos internos es 360°.

AEH + EHF + HFA + FAE = 360°

90° + EHF + 90° + FAE = 360°

EHF = 180° - FAE = 180° - BAC

BHC = EHF ya que estos ángulos son opuestos por el vértice.

Entonces, BHC = 180° - BAC.

Tracemos el punto H’ simétrico a H con respecto al eje BC. Entonces, sabemos que en el cuadrilátero ABH’C, BH’C = BHC = 180° - BAC Þ BH’C + BAC =  180°, condición suficiente para asegurar que ABH’C es inscriptible. Los puntos A, B y C ya están sobre la circunferencia C por lo tanto, H’ está sobre la misma circunferencia. Entonces H’ puede estar sólo en la circunferencia C. Como H es simétrico de H’ con respecto a BC, H puede estar solo en la circunferencia C’, que es la circunferencia simétrica a C con respecto a BC. Para trazar C’ podemos trazar O’ como el punto simétrico a O con respecto a BC, y luego por O’ trazamos la circunferencia C’ del mismo radio de C.

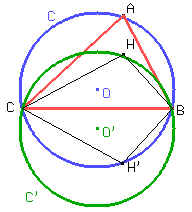
Si tomamos un punto H sobre C’, trazamos la perpendicular a BC por H (h), que corta a C en A₁ y A₂. Sea A₁ el que está del mismo lado de BC que H. El ortocentro de A₁BC está sobre h y sobre C’, y del mismo lado de BC que A₁ por lo tanto es el punto H.

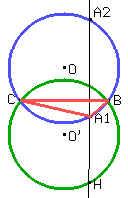
En conclusión, el lugar geométrico de H es la circunferencia cuyo centro es el punto simétrico a O con respecto a BC y cuyo radio es el mismo que el de C

Así terminamos la undécima clase de EduCabri, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar