Clase 16 - Problemas V

Esperamos sus mails en educabri@oma.org.ar.

Nivel Inicial

En caso de que no lo recuerden aquí va el problema que les propusimos la clase pasada:

Dada la siguiente figura formada por un triángulo equilátero y tres cuadrados, averiguar:

a) La medida de los ángulos de ACE.

b) La diferencia entre las áreas de DEF y BEI.

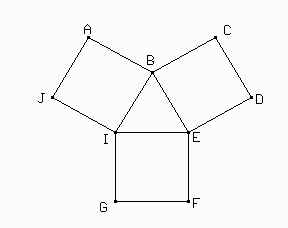
Comencemos calculando la medida de los ángulos de ACE.

Dado que AB = BI por ser ABIJ un cuadrado y BI = BE por ser BEI un triángulo equilátero, tenemos que AB = BI. Por tanto BAE = BEA. Además ABE = 90° + 60° = 150° por lo que BAE + BEA = 180° - 150° = 30°. Entonces BAE = BEA = 15°.

Como BEC = 45° (¿por qué?) llegamos a que AEC = 15° + 45° = 60°.

Calculemos, ahora, la medida de EAC para lo cual necesitamos conocer la medida de BAC. Dado que ABC = 360° - 90° - 60° - 90° = 120° y al ser AB = BC (¿por qué?) entonces BAC = BCA = (180° - 120°)/2 = 30°. Entonces EAC = 15° + 30° = 45°.

De aquí podemos deducir ECA = 75°.

Para calcular la diferencia entre las áreas de BEI y DEF, veamos que estos dos triángulos tienen igual área (en cuyo caso la diferencia es cero). El triángulo DEF es igual al triángulo ABC por simetría de la figura por lo que DEF = 120°. Fíjense que si partimos al triángulo DEF por la altura desde E y juntamos los dos triángulos resultantes formamos un triángulo equilátero de lado DE, y como DE = BE sus áreas son iguales. Les dejamos a ustedes la tarea de completar bien la demostración .....

Para que no se aburran les dejamos algunas actividades relacionadas con la figura del problema que tratamos esta clase ....

Problemas y actividades

1. Calcular la medida de BF.

2. Hallar el ángulo con que se cortan las rectas AI y CE.

3. Sabiendo que el perímetro de la figura es 18 hallar su área.

Nivel Avanzado

La clase pasada no les propusimos ningún problema así que aquí va uno. Les sugerimos que intenten resolverlo primero sin mirar la solución ...

Sea ABCD un cuadrilátero convexo con la siguiente propiedad:

Para cualquier punto P en el interior de ABCD la suma de las áreas de ABP y CDP es constante.

Demostrar que ABCD es un paralelogramo.

En este problema hay que tener en cuenta que, en principio, debemos trabajar con un cuadrilátero genérico. No basta probar que para un paralelogramo se cumple la propiedad del enunciado.

Lo que sí podemos particularizar es la posición del punto P dentro del cuadrilátero genérico ABCD ya que la propiedad del enunciado establece que se cumple para cualquier punto P interior.

Sea r una recta que interseca al cuadrilátero y que es paralela a AB, y sean P y Q puntos sobre la recta.

Según la condición del enunciado tenemos que: Área(ABP)+Área(CDP) = Área(ABQ)+Área(CDQ) Dado que PQ // AB sabemos que: Área (ABP) = Área (ABQ) pues ambos triángulos tienen igual base AB e igual altura.

Entonces, Área (CDP) = Área (CDQ). Como ambos triángulos tienen igual base CD, deben tener igual altura desde P y Q respectivamente; es decir, PQ // CD. Por tanto, CD // AB.

Cómo Área (ABP) + Área (CDQ) es constante, entonces Área (BCP) + Área (DAP) es constante para todo punto P en el interior de ABCD. Entonces de forma análoga, podemos demostrar que AD // BC.

O sea, que hasta aquí demostramos que de existir un cuadrilátero con la propiedad del enunciado, éste deberá ser un paralelogramo. Por tanto, nos falta probar que la propiedad del enunciado se cumple para cualquier paralelogramo.

Sea P un punto cualquiera en el interior del paralelogramo ABCD.

Calculemos las áreas de los triángulos: Área(ABP) = 1/2 AB . d(P, AB) Área(CDP) = 1/2 CD . d(P, CD) donde d(X, YZ) es la distancia del punto X a la recta YZ.

Entonces Área(ABP) + Área(CDP) = 1/2 AB . d(P, AB) + 1/2 CD . d(P, CD) y dado que AB = CD por tratarse de un paralelogramo, llegamos a que:

Área(ABP) + Área(CDP) = 1/2 AB . (d(P, AB) + d(P,CD))

Dado que d(P, AB) + d(P,CD) = d(A, CD) entonces:

Área(ABP) + Área(CDP) = 1/2 AB . d(A, CD) = 1/2 Área (ABCD) que es contante.

Con esto completamos la demostración ya que probamos que para cualquier paralelogramo se cumple la propiedad del enunciado pero para otro cuadrilátero no se cumple. Si se fijan, probamos que Área(ABP) + Área(CDP), además de ser constante, equivale a la mitad del área de ABCD.

Actividades y problemas

1. Dado un triángulo ABC, construir el triángulo DEF cuyos lados midan igual que las medianas de ABC. Calcular la relación entre las áreas de ABC y DEF.

2. Es posible hallar un triángulo ABC de modo que existe un punto P en su interior tal que cualquier recta que pase por P divida a ABC en dos figuras de igual área? Si existe tal triángulo hallarlo, de lo contrario justificar.

3. Sea ABCD un cuadrilátero tal que el área de ABD es 7 y el área de ACD es 9. Si M es punto medio de BC. Hallar el área de AMD.

Será hasta la próxima. Hagan las actividades e intenten resolver los problemas. No se olviden de contestar la encuesta que se encuentra al final de la clase !!!

Esta fue la décimo sexta clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar