Clase 15 - Problemas IV

Esperamos sus mails en educabri@oma.org.ar.

Nivel Inicial

Les recordamos el problema que les propusimos la clase pasada:

Construir dos cuadrados tal que la uno tenga 5 veces el área del otro.

En este problema es importante no confundir que un cuadrado tenga 5 veces el área de otro, a que sea 5 veces más grande.

Si x es la medida del lado del cuadrado menor entonces su área es x², por lo que el área del cuadrado mayor será 5x². Si el lado del cuadrado más grande es y entonces su área será, también, y². Entonces:

5x² = y²

. x = y

Lo que debemos hacer, entonces, es construir un segmento que mida veces x. No vale construir un segmento que mida 2,236 veces x, pues aunque 2,236 y están muy próximos, no son exactamente iguales. La idea es construir un triángulo rectángulo de catetos x y 2x pues sabemos al realizar Pitágoras que su hipotenusa mide . x. Veamos como realizar la construcción.

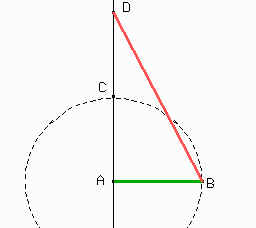Sea AB el segmento de lado x. Por A se traza una recta perpendicular a AB que corta a la circunferencia centrada en A y radio AB, en el punto C. Como son radios de la circunferencia tenemos que AC = AB. Sea D el simétrico de A con respecto a C. Entonces como CD = AC tenemos que AD = 2AB. Por Pitágoras: AB² + (2AB)² = 5AB² = BD²

Por lo tanto BD = . AB como queríamos. Lo único que nos resta es construir los cuadrados, que se lo dejamos a ustedes.

Problemas y actividades

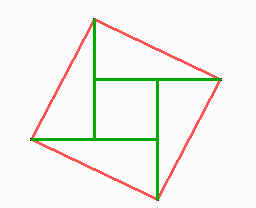
1. Justificar la siguiente construcción del problema de la clase de hoy, demostrando que la figura roja es un cuadrado:

2. Construir un triángulo equilátero que tenga el triple de área que otro.

3. Dado un triángulo equilátero construir un hexágono regular de igual área.

Les dejamos el problema que vamos a tratar la clase que viene para que lo vayan pensado ...

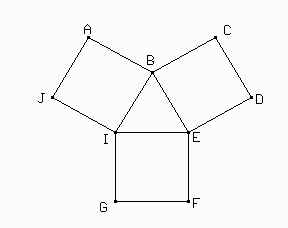
Dada la siguiente figura formada por un triángulo equilátero y tres cuadrados, averiguar:

a) La medida de los ángulos de ACE.

b) La diferencia entre las áreas de DEF y BEI.

Nivel Avanzado

Les recordamos el problema que propusimos la clase pasada:

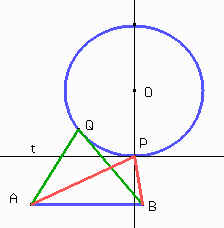
a) Dada una circunferencia K y dos puntos A y B, de modo que la recta AB no corte a la circunferencia, construir el punto C sobre K de modo que el área de ABC sea mínima.

b) Sea D sobre K de modo que el área de ABD sea máxima. Hallar la diferencia entre las áreas de ABD y ABC en función de AB y del radio de K.

Para que el área de ABC sea mínima, debemos minimizar la altura desde C a AB ya que la base AB es constante. Tracemos una recta tangente a la circunferencia que sea paralela a AB.

Por el centro O de la circunferencia K trazamos una recta perpendicular a AB que interseca a K en P (el corte más próximo a AB). Por P trazamos una recta paralela a AB que será tangente a K por ser perpendicular al radio OP. Si tomamos un punto Q sobre la circunferencia, distinto de P, Q quedará en el semiplano determinado por t, que no contiene a A. Entonces la distancia desde Q a AB será mayor que la distancia desde P a AB. Por lo tanto P es el punto C que buscábamos.

Del mismo modo podemos demostrar que D (el punto tal que ABD tiene área máxima) es el diametralmente opuesto a P. Entonces:

Área(ABD) - Área(ABC) = 1/2(AB . Hd) - 1/2(AB . Hc) = 1/2 AB (DC) = AB . r

donde r es el radio de K.

Les dejamos algunos problemas y actividades relacionadas con el tema de hoy ...

1. Dada un circunferencia K y un punto A en su interior, distinto del centro, construir los puntos B, C y D sobre K de modo que el área de ABCD sea máxima.

2. Sea ABC un triángulo y sea D un punto en su interior tal que:

• AB = 5 y CD = 4

• El área de ACBD es 5.

Hallar el ángulo que forma la recta CD con la recta AB.

3. Dada una circunferencia construir el triángulo de área máxima inscripto en ella.

Será hasta la próxima. Hagan las actividades e intenten resolver los problemas. No se olviden de contestar la encuesta que se encuentra al final de la clase !!!

Esta fue la décimo quinta clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar