Clase 10 - Homotecia

Esperamos sus mails en educabri@oma.org.ar.

 

El problema que les contamos a continuación, pertenece al nivel B y formó parte de la segunda ronda de la 10ma Competencias de Clubes Cabri.

Dado un triángulo ABC construir una circunferencia que pase por C, sea tangente a AB, tal que si D y E son los puntos de intersección entre la circunferencia y CA y CB respectivamente, entonces DE sea paralela a AB.

Tal vez lo hayan resuelto alguna vez. Si no es el caso; deténganse unos minutos a ver si les sale. Al final de ésta clase, vamos a ver cómo se puede abordar este problema usando homotecia.

¿Qué es la homotecia?

Creen dos puntos básicos y llámenlos I y O. Construyan el punto medio entre I y O. Llámenlo M y píntenlo de rojo. Marquen el lugar geométrico de I y de M al mover I. (Para marcar el lugar geométrico de dos puntos hay que mantener Shift apretado cuando marcan los dos primeros puntos). Muevan lentamente el punto I por la pantalla. De esta forma verán un dibujo negro y uno rojo.

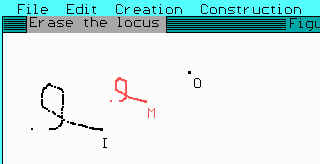
4. ¿Cómo son esas dos figuras entre sí?

Estas figuras se llaman homotéticas. A cada punto I del plano se le asigna un punto P en la recta IO de tal forma que PO / IO sea constante. En el caso anterior MO / IO = 1/2. El punto O se llama centro de homotecia.

Como habrán notado la homotecia no hace más que agrandar o achicar una figura, sin cambiarle la forma ni la orientación. Pero, ¿cómo podríamos probar esto, aunque sea en los objetos básicos?

Homotecia de un segmento

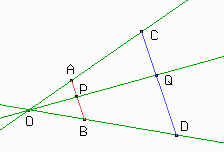
Vamos a aplicarle al segmento AB una homotecia de razón r con centro en O. Los puntos C y D son los homotéticos de A y B. Como CO / AO = DO / BO = r, por el Teorema de Thales, los segmento AB y CD son paralelos; y además, los triángulos COD y AOB son semejantes. Entonces, CD / AB = r, o lo que es lo mismo, CD = r.AB Para cualquier punto P del segmento AB, llamamos Q a la intersección de CD con la recta OP. Como las rectas AB y CD son paralelas, por el Teorema de Thales, QO / PO = CO / AO = r, entonces Q es homotético de P.

Esto nos prueba que la homotecia aplicada al segmento AB, da por resultado el segmento CD, ya que cada punto del primero se transforma en uno del segundo.

En definitiva, se puede ver que siempre la figura homotética de un segmento es otro segmento paralelo al original, cuya longitud es la del primero multiplicada por la razón de homotecia.

Para demostrar que la homotecia de un triángulo da por resultado otro triángulo, semejante al original, basta hacer la homotecia por separado a los tres segmentos que forman sus lados.

Más general aún, se puede demostrar de una forma parecida, que al hacer la homotecia de un polígono se obtiene otro polígono semejante al original, donde la razón de semejanza es igual a la razón de la homotecia.

Homotecia de una circunferencia

Demostrar que la figura homotética a una circunferencia C es otra circunferencia es un poco más difícil. Veamos cómo se hace.

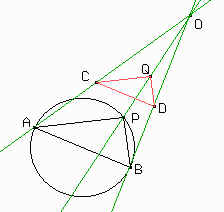Tomamos un diámetro AB de la circunferencia y un punto P sobre la misma. Hacemos la homotecia del triángulo ABP que nos da el triángulo CDQ. Como el ángulo APB está inscripto en una semicircunferencia entonces mide 90° y como CDQ es semejante entonces tenemos que CQD = 90°. Al mover el punto P por la circunferencia el punto Q describirá un arco capaz de 90°. Es decir que Q describe otra circunferencia. Además la razón entre los diámetros es igual a la razón entre AB y CD, o sea, igual a la razón de homotecia. En conclusión la homotecia de la circunferencia que pasa por ABP nos da la circunferencia que pasa por CDQ.

La conclusión puede ser simple: Dos figuras homotéticas son siempre semejantes.

Volvamos, ahora, al problema que les contamos a principio de esta clase.

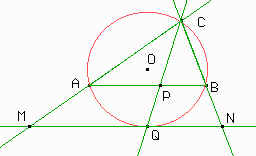Primero trazamos la circunferencia circunscrita a ABC y llamemos O a su centro. La recta perpendicular a AB por O corta a la circunferencia en Q como muestra la figura. Por Q trazamos una paralela a AB (que será perpendicular a OQ) que corta a AC y a BC en M y N respectivamente. Entonces MN es tangente a la circunferencia y además AB // MN, por lo que esta figura es homotética a la que queremos construir, y C es el centro de homotecia.

Por lo tanto, si P es la intersección de QC con AB, entonces P será el punto de tangencia de la circunferencia que deseamos construir con el segmento AB. Ahora es más fácil hacer la figura. Basta con trazar una perpendicular a AB por P, y su intersección con la mediatriz de CP determinará el centro de la circunferencia a construir. ¿Por qué?

Existen otras formas de resolver este problema, que no son menos interesantes que la que acabamos de mostrarles. Una de ellas también se basa en hallar primero el punto P de tangencia, pero para hacerlo demuestra que CP es bisectriz del ángulo C. Intenten demostrarlo ...

Para terminar esta clase veremos que dos homotecias sucesivas aplicadas a una misma figura puede reemplazarse por una sola homotecia.

Llamemos F a la figura original, y F1 a la figura obtenida en la primer homotecia, de razón r, con respecto a un centro O. La figura F1 será entonces semejante a F, sin cambiar la orientación, y la razón entre ambas será r, como lo demostramos al principio de la clase. Sea F2 la figura que se obtiene al hacer una homotecia de razón p con centro O1 de F1. Esta figura será semejante a F1 y la razón de semejanza será p. Por lo tanto, F2 es semejante a F, con razón r.p, y poseen la misma orientación. Es decir, son homotéticas con centro O2.

Bueno, antes de que se vayan les dejamos unos problemitas para que piensen. No se olviden de contestar la encuesta que está al final de la clase !!!

Problemas

1. Dados una circunferencia y un triángulo, construir un triángulo inscripto en la circunferencia que sea semejante al primero.

2. Se tiene un triángulo ABC. Construir un cuadrado que tenga un lado sobre AB, un vértice sobre BC y el otro sobre CA.

3. Dado un triángulo ABC, sea A´B´C´ una homotecia del ABC, de centro O y radio r. ¿Cuál es la relación entre las áreas de A´B´C´ y ABC?

4. Dado un pentágono ABCDE, construir un pentágono cuyos lados midan lo mismo que las diagonales de ABCDE.

Así terminamos la décima clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.

.

EduCabri OmaNet Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar mensajes webmaster@oma.org.ar