
Clase 7 - Triángulos de igual área
Esperamos sus mails en educabri@oma.org.ar.
Clase 7 - Triángulos de igual área
Esperamos sus mails en educabri@oma.org.ar.
Vamos a comenzar esta clase enunciando un problema que apareció en una nacional en primer nivel hace mucho tiempo (casi 6 años).
Sobre tres vértices de un rectángulo se encuentran paradas tres hormiguitas, una en cada vértice. La hormigas se mueven por turnos del siguiente modo: cuando una hormiga se mueve las otras dos se quedan quietas y la que se mueve lo hace por la recta paralela al segmento determinado por las otras dos hormiguitas. ¿Es posible que luego de algunos turnos las tres hormigas queden paradas en tres de los puntos medios de los lados del rectángulo?
¿Pudieron hacerlo? Si no, no importa, porque ahora veremos algunas ideas que les pueden ayudar.
Construyan un triángulo ABC con el Cabri y luego por C tracen una recta paralela a AB. Con point on object ubiquen un punto D sobre dicha recta y construyan el triángulo ABD.
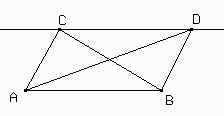
Las distancias desde C y D a la recta AB son iguales porque CD // AB. El área del triángulo ABC es igual a la mitad del producto entre AB y la distancia desde C a AB; y el área de ABD es igual a la mitad del producto entre AB y la distancia desde D a AB. Es decir, ¡las áreas de ABC y de ABD son iguales!
Ahora estamos en condiciones de resolver el problema que enunciamos al principio. Antes de seguir leyendo traten de hacer el problema nuevamente, a ver si ahora les sale. Tengan en cuenta que las hormigas pueden moverse, en su turno, para el lado que deseen y todo lo que deseen.
La cuestión es la siguiente. Cada vez que se mueve una hormiga el triángulo que queda determinado por las tres hormigas no cambia de área. Es como si la hormiga estuviera parada en el punto C y luego caminara hasta el punto D.
Es decir, que el triángulo que formaban las hormigas al principio tiene que tener la misma área que el que formen al final. El área del triángulo formado por 3 vértices del rectángulo tiene la mitad del área del mismo. Veamos lo que sucede con el triángulo de los puntos medios:
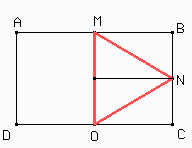
Como vemos en la figura el triángulo MNO tiene menor área que la mitad del rectángulo. De hecho, su área es la cuarta parte del área de ABCD. Demuéstrenlo ....
En conclusión las hormigas no pueden ubicarse en tres de los puntos medios del rectángulo.
¿Qué opinan si vemos otro problema relacionado con áreas de triángulos?
Sobre el lado BC de un paralelogramo ABCD se halla el punto P de modo que el área de ABPD sea 12 y el área de PCD sea 8. La recta PD interseca a la recta AB en Q. Hallar el área del triángulo CPQ.
Un problema muy parecido a éste apareció en la Nacional de Bariloche, tres años atrás. Les aconsejamos que intenten resolverlo primero por su cuenta antes de ver la solución que les proponemos. Tengan en cuenta que no se nos da ningún dato sobre los lados del paralelogramo por lo que deben resolver el problema para el caso general.
¿Salió? Sino, buen intento. Muchas veces aprendemos más intentando resolver un problema, aunque no nos salga, que leyendo de primera la solución.
Hagamos una figura para ayudarnos a ver mejor las cosas. Es importante que sepan que la figura no respeta las relaciones del enunciado pues solamente la utilizaremos para ubicarlos puntos y triángulos.
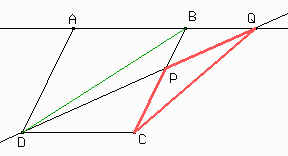
El área de todo el paralelogramo es 20 y dado que los triángulos ABD y CDB son iguales (¿Por qué?) entonces el área de CDB es 10.
Como ABCD es un paralelogramo entonces BQ // CD. Por este motivo las áreas de BCD y de CDQ son iguales. Es decir que: Área(CPD) + Área(CPQ) = Área(CDQ) = 10. Por lo tanto el área de CPQ es 2.
Ahora un último problema, un poco distinto a los anteriores.
Dado un triángulo ABC y M el punto medio de AB. La distancia de M a la recta AC mide 1 mientras que la distancia de M a la recta BC mide 2. Demostrar que AC mide el doble de BC.
Para demostrar el problema recuerden que en el enunciado no hay ninguna especificación sobre la medida de los lados de ABC, ni sobre su área; por lo que hay que probar el caso general.
No daremos aquí la demostración completa del problema. Sin embargo, les daremos algunas pistas para que usen en caso que lo necesiten. Lean las pistas de a una, y no pasen a la siguiente sin haber intentado resolver la parte anterior.
Demuestren que las áreas de AMC y BMC son iguales.
Calculen el área de AMC usando a AC como base, y calculen el área BCM usando BC como base. ¿Se les ocurre algo?
Usen los puntos 1 y 2 juntos. ¿Salió?
Ahora les dejamos algunos problemas para que hagan. Si tienen alguna duda o quieren mostrarnos las soluciones a las que llegaron, no duden en escribirnos.
Problemas
1. Sea AB un segmento y sea C y D puntos del mismo lado de la recta AB. Sabiendo que el área de ABC es igual al área de ABD demostrar que AB es paralela a CD.
2. Dado un cuadrilátero convexo construir un triángulo de igual área.
3. Dado un cuadrilátero convexo ABCD construir una recta que pase por A y que divida a la figura en dos de igual área.
4. En un triángulo ABC de área 36 se trazaron: el segmento DE que une los puntos medios de los lados de AB y AC, y dos rectas paralelas entre sí por D y E que cortan al lado BC en F y G respectivamente, de modo que el área del triángulo EGC resultó igual a 5. Calcular el área del triángulo DBF.
5. ABCD es un rectángulo con AB= 5 y CB = 3. Sea P sobre AB y en AP de modo que DN sea perpendicular a AP. Calcular el valor de AP.DN.
Así terminamos la séptima clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.
Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntenos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .
También nos gustaría saber tu opinión sobre esta clase. Te pedimos que te tomes unos instantes y contestes estas preguntas. Con tu ayuda podremos hacer un curso cada vez mejor.
|