Clase 5 - Ángulos entre paralelas

Esperamos sus mails en educabri@oma.org.ar.

 

En el curso del 98, de las primeras clases de introducción pasamos directamente a los puntos notables de un triángulo. Y este año comenzamos con algunos temas, tal vez un poco complicados. Por esta razón queremos abordar en esta clase las propiedades de los ángulos entre paralelas, para asegurarnos que todos puedan entender bien los temas que hemos tocado en clases anteriores y en clases que veremos más adelante.

Parte 1 - Actividades

1-1 Ángulos suplementarios y ángulos opuestos por el vértice

1. Trazá dos rectas que se corten en un punto P.
2. Marcá y medí los cuatro ángulos que se forman. ¿Qué relación hay entre éstos ángulos?

Decimos que los ángulos A1 y A2 son opuestos por el vértice y son congruentes. También B1 y B2 son opuestos por el vértice y, por lo tanto, congruentes.

Decimos que los ángulos A1 y B1 son suplementarios y la suma de sus medidas es 180^o.

3. ¿Cuáles otros tres pares de ángulos son suplementarios?

1-2 Ángulos entre paralelas

1. En la figura anterior, construí una recta paralela a alguna de las dos.
2. Marcá y medí los cuatro ángulos que quedan formados.

3. ¿Qué relación hay entre las medidas de A1 y C1?
4. Decimos que los ángulos A1 y C1 son correspondientes y resultan congruentes. ¿Qué otros tres pares de ángulos correspondientes hay?

A partir de esta propiedad de los ángulos correspondientes entre paralelas y las dos de la actividad 1.1, se pueden deducir las siguientes:

5. ¿Qué relación hay entre las medidas de A1 y D2? ¿Podés demostrarlo usando las propiedades anteriores?
6. Decimos que los ángulos A1 y D2 son conjugados externos. ¿Cuál es el otro par de ángulos conjugados externos?
7. ¿Qué relación hay entre las medidas de B2 y C1? ¿Podés demostrarlo?
8. Podés adivinar cómo se llaman... Sí, decimos que los ángulos B2 y C1 son conjugados internos. ¿Cuál es el otro par de ángulos conjugados internos?
9. ¿Qué relación hay entre las medidas de A1 y C2? ¿Podés demostrarlo?
10. Decimos que los ángulos A1 y C2 son alternos externos. ¿Cuál es el otro par de ángulos alternos externos?
11. ¿Qué relación hay entre las medidas de B2 y D1? ¿Podés demostrarlo?
12. También podés adivinar ... Decimos que los ángulos B2 y D1 son alternos internos. ¿Cuál es el otro par de ángulos alternos internos?

1-3 Ángulos de un paralelogramo

Un paralelogramos es un cuadrilátero con los pares de lados opuestos paralelos.

1. Construí un paralelogramo, marcá y medí sus ángulos interiores.
2. ¿Qué relación hay entre las medidas? ¿Por qué?

1-3 Ángulos de un trapecio

Un trapecio es un cuadrilátero con un par de lados opuestos paralelos.

1. Construí un trapecio, marcá y medí sus ángulos interiores.
2. ¿Qué relación hay entre las medidas? ¿Por qué?

Parte 2. Problemas

2.1 Un barco navega entre dos orillas paralelas, siguiendo el recorrido de la figura.

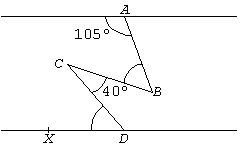
Se sabe que <ABC = <CDX y <CBD = <CDB. Calcular <ABC.
(<ABC signfica "el ángulo ABC")

2.2 Sea ABC un triángulo con <B=35^o, <C=28^o. Se traza por A una paralela r al lado BC. La mediatriz de AC corta a r en D y la mediatriz de AB corta a r en E. Queda formado el cuadrilátero BCDE. Hallar sus ángulos interiores.

2.3 En un triángulo ABC que tiene <B = 37^o y <C = 38^o se marcan los puntos P y Q en el lado BC de manera tal que <BAP = <PAQ = <QAC. Se traza por B una paralela a AP y se traza por C una paralela a AQ, que corta a la anterior en D. Calcular <DBC.

Así terminamos la quinta clase de Educabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar