Clase 4 - Polígonos de igual área

Esperamos sus mails en educabri@oma.org.ar.

 

Comencemos esta clase directamente enunciando el problema en cuestión.

Dados dos polígonos A y B construir un polígono C, semejante al polígono B y que tenga la misma área que A.

Demostremos primero que dado cualquier polígono se puede construir un triángulo de igual área. Dado un polígono de n lados, con n > 3, sean A, B, C y D cuatro vértices consecutivos del mismo.

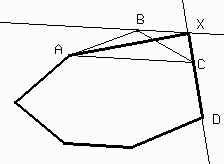
Por B trazamos una recta paralela a AC, que interseca a la recta CD en X. El triángulo ABC tiene la misma área que el triángulo AXC pues ambos poseen la misma base AC y la altura desde B y desde X es la misma por ser BX // AC.

Entonces el nuevo polígono, remarcado en la figura, con vértices A, X y D además de los que comparten ambos polígonos, tiene la misma área que la figura original y posee n-1 lados. Repitiendo este proceso n-3 veces obtendremos un triángulo de igual área que el polígono dado.

Pero, ¿de qué nos sirve obtener dicho triángulo? Supongamos, por el momento, que podemos construir dado un polígono un cuadrado de igual área. Entonces podremos tener dos cuadrados X e Y de igual área que los polígonos A y B respectivamente.

Si construimos el polígono C de modo que la razón de semejanza con B sea la misma que la razón de semejanza entre X e Y, entonces tenemos que:

Área(C) / Área(B) = Área(X) / Área(Y) = Área(A) / Área(B)

Es decir que el área de C será igual que el área de A.

Veamos entonces como podemos construir un cuadrado de igual área que un triángulo dado. Sea ABC el triángulo y sean M y N los puntos medios de AB y AC respectivamente. El punto P es el simétrico de M con respecto a N.

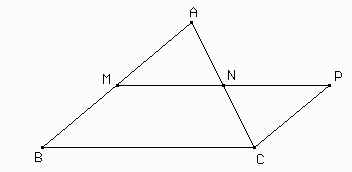
Como MN es base media, entonces es paralelo a BC y además 2MN=BC. Por tanto, MP y BC miden lo mismo y son paralelas. Es decir, BMPC es un paralelogramo. Sean R y S los pies de las perpendiculares a la recta BC desde M y P respectivamente. El rectángulo MPSR tendrá igual área que BMPC pues ambos tienen la misma base y la misma altura.

Ahora, nos falta construir un cuadrado de igual área que MPSR.

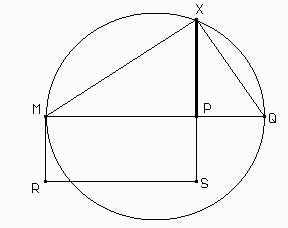
Trazamos la circunferencia de centro P y radio PS, que interseca a la prolongación de MP en Q. Entonces PQ = PS. La circunferencia de diámetro MQ interseca a la prolongación de PS en X. Por ser MXQ un ángulo inscrito en una semicircunferencia tenemos que MXQ = 90°.

Si XMP = x entonces MQX = MXP = 90° - x. Por tanto, MXP y XQP son semejantes de donde deducimos que MP / PX = PX / PQ; o puesto de otro modo MP.PQ = PX². Como MP.PQ es el área del rectángulo MPSR entonces PX será el lado del cuadrado que buscábamos.

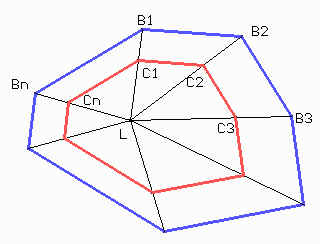
Nos resta ver como construir efectivamente el polígono C. Tomemos un punto L en el interior del polígono B y llamemos a sus vértices B1, B2, ...., Bn.

Sea AC el lado del cuadrado X, que tenía la misma área que el polígono A; y sea AB el lado del cuadrado Y, que tenía igual área que el polígono B. Por el otro lado, D es un punto en la prolongación de AB de modo que BD mida lo mismo que LB1. Sea E la intersección de la recta AC con la recta que pasa por D y es paralela a BC. Por el teorema de Tales CE/BD será la razón de semejanza entre el polígono B y el C.

Entonces si C1 es un punto en la semirrecta LB1 de modo que LH=CE y realizamos el mismo procedimiento para los otros vértices del polígono B, obtendremos un polígono C1C2....Cn semejante a B y con la misma área que el polígono A.

Para terminar esta clase les dejamos algunos problemas para que practiquen.

Problemas

1. Dado un cuadrado construir un triángulo equilátero de igual área. ¿Puedes hallar un procedimiento distinto al que enseñamos en esta clase para hacerlo?

2. Dado un cuadrilátero ABCD construir un triángulo de igual área y que posea un ángulo de 45°.

3. Sean ABC y DEF dos triángulos. Construir un cuadrado cuya área sea igual a la suma de las áreas de ambos triángulos.

Esta fue la cuarta clase de EduCabri 2000, el curso de Cabri por Internet para usuarios de Omanet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar