Clase 2 - Reflexiones y desigualdad triangular

Esperamos sus mails en educabri@oma.org.ar.

 

En esta clase veremos algunas construcciones que se valen del uso de reflexiones y se basan en la conocida desigualdad triangular. Ésta desigualdad dice básicamente que dados tres puntos A, B y C se cumple que AB + BC > AC; o dicho de otro modo, la suma de dos lados de un triángulo es mayor o igual que el tercer lado. La igualdad se cumple sí y sólo sí A, B y C están alineados en ese orden.

Esta aparentemente sencilla desigualdad y la simpleza de las reflexiones permiten resolver problemas realmente complejos de una forma breve y elegante. Bueno, basta de charla y vayamos directo a los problemas.

Problema 1. Dada una recta r y dos puntos A y B del mismo lado con respecto a ella se pide encontrar el camino de longitud mínima que una a A con B, tocando en un punto a la recta r.

Sea A₁ el simétrico de A con respecto a r, sea C la intersección de BA₁ y r, y sea D otro punto cualquiera sobre la recta r.

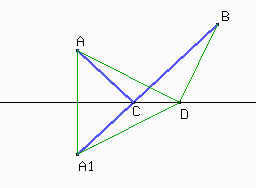
Debido a que A₁ es simétrico de A respecto de r, tenemos que AC = A₁C y AD = A₁D. Si el camino ADB es el mínimo entonces también debe ser mínimo A₁D + DB. De acuerdo con la desigualdad triangular ésto sucede solamente cuando A₁, D y B están alineados. Por tanto, el camino es mínimo cuando D se ubica donde está C.

Problema 2. Sea ABC un triángulo acutángulo y P un punto sobre el lado AB. Construir los puntos Q y R sobre AC y BC respectivamente de modo que el perímetro de PQR sea mínimo.

En es problema es mucho más complicado ver como obtener la desigualdad triangular. De todas formas, la estrategia es similar a la del primer problema: hacer reflexiones.

A₁ es el simétrico de A con respecto a BC y B₁ es el simétrico B con repecto a CA₁.

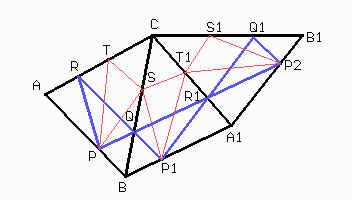
La misma reflexión hacemos con el triángulo PST como lo indica la figura. El punto P₂ se construye en A₁B₁ de modo que PB = B₁P₂. Las intersecciones de PP₂ con BC y CA₁ determinan los puntos Q y R₁ respectivamente.

R es el simétrico de R₁ con respecto a BC, P₁ es el simétrico de P con respecto a BC y Q₁ es el simétrico de Q con respecto a A₁C. Debido a las simetrías realizadas tenemos que RQ = R₁Q y que P₂R₁ = P₁R₁ = RP. Del mismo modo sabemos que TS = T₁S y que T₁P₂ = TP.

Juntando todo esto llegamos a que el perímetro de PQR es igual a P₂P y que el perímetro de PST es igual al camino PST₁P₂.

Veamos, ahora, que para cualesquier S y T el perímetro de PQR es menor o igual que el de PST o de modo equivalente demostraremos que P₂P es menor que el camino PST₁P₂.

Pero, ¿cómo conectamos esto con la desigualdad triangular? Bueno, sabemos que PS + ST₁ es mayor o igual que PT₁. Por el otro lado PT₁ + T₁P₂ es mayor o igual que P₂P de donde tenemos que PS + ST₁ + T₁P₂ es mayor o igual que P₂P como queríamos probar. La igualdad se cumple sólo cuando P, S T₁ y P₂ están alineados; es decir cuando S es Q y T₁ es R₁. Por tanto PQR es el triángulo de perímetro mínimo.

Problema 3. Sea ABC un triángulo con AB = AC y sean R y S sobre AB y AC respectivamente. Demostrar que existe un triángulo de lados RC, RS y SB.

En este problema, a diferencia de los dos anteriores, se nos pide directamente que demostremos que tres segmentos pueden formar un triángulo. Esto nos deja dos salidas. Una es calcular de forma analítica los segmentos y probar que cumplen con la desigualdad triangular, lo cual es bastante engorroso.

La otra salida, que es la que utilizaremos, es mostrar como dicho triángulo puede construirse. Para hacerlo recurriremos a una idea feliz: construir una figura en el espacio. ¡Sí, leyeron bien, una figura en 3D para resolver un problema en el plano!

Consideremos un tetraedro DEFG con DEF equilátero de lado igual que BC y G de modo que GD = GE = GF = AB.

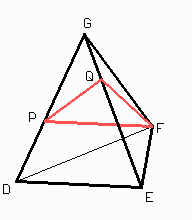
Sea Q en GE de modo que GQ = AS y sea P en GD de modo que GP = AR. Entonces PQ = RS porque GQP y ASR son triángulos congruentes. También tenemos que QF = BS por ser GQF congruente con ASB. Y Finalmente PF = CR pues PFG y CRA son congruentes. Juntando toda la información tenemos que FPG es un triángulo de lados RS, BS y CR como pedía el enunciado.

Concluyendo esta clase les dejamos 4 problemas para que practiquen; los dos primeros son más bien fáciles, mientras que los últimos son más avanzados. Y no se olviden, cualquier duda que tengan, ¡Comuníquense con nosotros!

Problemas

1. Dadas dos rectas paralelas r y s y dos puntos A y B comprendidos entre ambas rectas. Construir dos puntos C y D en r y un punto E en s de modo que AC + CE + ED + DB sea mínimo.

2. Demostrar que cualquier camino poligonal que una a dos puntos A y B tiene mayor longitud que el segmento AB.

3. Sea ABC un triángulo equilátero y sea P, Q y R sobre AB, BC y AC respectivamente. Demostrar que existe un tetraedro cuyos lados tengan longitud AQ, BR, CP, RP, RQ y PQ.

4. Construir el triángulo inscripto a un triángulo acutángulo que sea de perímetro mínimo.

Esta fue la segunda clase de EduCabri 2000, el curso de Cabri por Internet. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.

Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .

EduCabri OmaNet	Internet vía OmaNet    www.oma.org.ar/omanet | omanet@oma.org.ar
mensajes webmaster@oma.org.ar