
Clase 1 - Demostrando con el Cabri
Esperamos sus mails en educabri@oma.org.ar.
Clase 1 - Demostrando con el Cabri
Esperamos sus mails en educabri@oma.org.ar.
¿Qué es una demostración? Y más aún, ¿qué es una demostración usando el Cabri? En esta clase introductoria intentaremos responder a estas dos preguntas pues son fundamentales, nos sólo para las competencias, sino también para poder sacarle el mayor jugo posible a los problemas.
La demostración de un problema no es solamente la exposición de los pasos que uno realizó para llegar al resultado. Es más que nada, la explicación de por qué uno utilizó esos pasos, de los teoremas e ideas que avalan el procedimiento utilizado para resolverlo.
Cuando uno demuestra algo debe imaginar que le está explicando la justificación a otra persona que no entiende nada, o muy poco; y debe imaginar las preguntas que le haría, a uno, esa persona.
¿Qué teoremas
utilizaste?
¿Usaste alguna otra idea? ¿Cuál? ¿Por qué?
¿Esa idea sirve para un caso particular o también para el caso
general que pide el problema?
Si es un problema de geometría, ¿que pasa si se cambia la
figura?
¿Hay otra forma mejor de resolver el problema?
En fin, cualquier pregunta que haría alguien que quisiera saber con certeza la solución del problema.
Ahora, ¿cómo es una demostración utilizando el Cabri?
Cuando uno quiere hacer una construcción con el Cabri, no basta con hacerla a ojo. Para que la construcción esté bien hecha no se debe desarmar al mover la figura y debe seguir cumpliendo las condiciones que pedía el problema.
Otro error muy común es utilizar el comando Measure para medir segmentos y ángulos y justificar el problema basándose en los datos así obtenidos. La idea de medir sirve solamente para notar regularidades, pero de ningún modo sirve para demostrar un problema.
Para fijar mejor todas estas ideas, les proponemos un problema. Intenten resolverlo por su cuenta antes de seguir adelante. Después les mostraremos una demostración bien hecha del problema y otra que no lo está. Fíjense en cual de las dos encaja mejor la que hicieron ustedes, para ver en que andan más flojos.
Dado un rectángulo ABCD y un punto E en AB construir el rombo EFGH donde F, G y H pertenecen a BC, CD y DA respectivamente. Explicar los pasos de la construcción y justificar porque el cuadrilátero EFGH construido es un rombo.
Así, NO
|
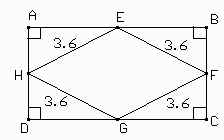 |
Aquí los errores son muchos y muy burdos, pero sirven para aclarar mejor qué no se tiene que hacer:
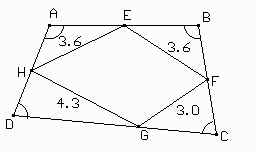 |
1. El rectángulo hay que construirlo de modo que no
se desarme la figura al mover los puntos. 2. En ningún lugar del enunciado dice que E es el punto medio de AB. Esto es un caso particular. Tenemos que hacer de cuenta que viene alguien con un rectángulo y un punto E sobre el lado AB y nos dice "Ahora construí el rombo EFGH". 3 y 4. Aquí también se desarma la figura al correr de lugar los puntos. |
5 y 6. Medir los segmentos no sirve de nada en la demostración, pues bien podría pasar que los lados midieran 3.61, 3.62, 3.59 y 3.58 y el Cabri seguiría marcando en todos los casos 3.6. De todas formas, aún si midieran lo mismo, medir no sirve para hacer la demostración pues en otra figura podrían no medir lo mismo. Es decir, estaríamos trabajando en un caso particular y no en el caso general que pide el enunciado.
Así, SÍ
Veamos ahora como debe ser la demostración del problema:
| Primero construimos el rectángulo ABCD de la siguiente forma: trazamos el segmento AB y por A y por B construimos las rectas perpendiculares a AB (r y s respectivamente). Con Point on object colocamos el punto C en s y luego trazamos la perpendicular a BC por C cuya intersección con r da el punto D. Colocamos el punto E en AB utilizando, también, Point on object. | 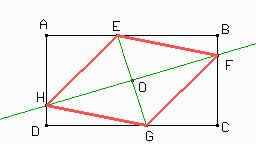 |
Sea O el centro del rectángulo (la intersección de las diagonales de ABCD). G es la intersección de la recta EO y CD. Como O es la intersección de las diagonales del rectángulo entonces AO = OC. Además, como AB // CD, por ser alternos internos entre paralelas EAO = OCG y AEO = OGC. Entonces, por el criterio de congruencia de triángulos que nos dice que: dos triángulos son congruentes si tienen los mismos ángulos y un par de lados congruentes, AEO y OGC son congruentes, de donde obtenemos que EO = OG.
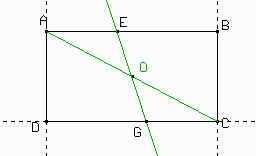 |
La mediatriz de EG, que pasará por O, interseca a
las rectas BC y AD en F y H respectivamente. Veamos por qué EFGH es un rombo: Por estar en la mediatriz de EG tenemos que HE = HG y EF = FG. Del mismo modo que demostramos antes, OF = HO y además EG es perpendicular a FH. Es decir, que EG es mediatriz de HF, con lo que EH = EF. Por lo tanto los cuatro lados de EFGH miden lo mismo, es decir es un rombo, como queríamos demostrar. |
Esperamos que la solución de ustedes haya sido parecida a la que acabamos de mostrarles. En caso de que tengan algún de los errores que aparecen en la solución mal hecha, les recomendamos que vuelvan a leer esta clase y que practiquen resolviendo problemas y escribiendo las demostraciones. Luego fíjense si cumplen con los requisitos de una buena demostración que fuimos enunciado a lo largo de la clase; y cualquier pregunta que tengan, ¡No duden en comunicarse con nosotros!
Problemas
1. Construir un triángulo de modo que sus ángulos midan 15°, 60° y 105°.
2. Dado el triángulo rectángulo ABC, con C = 90°, AC = 1 y BC = 2, hallar la distancia de C a la recta AB.
Esta fue la clase 1 de EduCabri 2000, el curso interactivo de geometría con Cabri. Esperamos que les haya gustado. La semana que viene, ofreceremos una nueva clase.
Mientras tanto, es el turno de ustedes. Queremos que sigan las actividades y hagan los problemas. Cuéntennos lo que consiguieron y pregunten lo que no les salió. Envíen sus preguntas, dudas, sugerencias, experiencias y propuestas. Nuestra dirección es educabri@oma.org.ar .
| Internet vía OmaNet www.oma.org.ar/omanet | omanet@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |